题目内容
【题目】已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
, ![]() 与
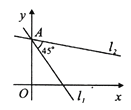
与![]() 在A点相交所形的 夹角为45°(如图所示),则直线
在A点相交所形的 夹角为45°(如图所示),则直线![]() 的函数表达式为____________.
的函数表达式为____________.
【答案】y=![]() x+2
x+2
【解析】
由题意得A(0,2),B(1,0),作BD⊥AB交直线12于D,作DC⊥x轴于C,利用全等三角形的性质求出点D坐标,再运用待定系数法即可解答.
解:
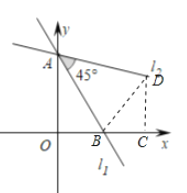
解:如图:作BD⊥AB交直线l2于D,作DC⊥x轴于C,
由题意得A(0,2),B(1,0)
∵∠DAB=45°
∴∠ADB=45°,
∴BD=AB
∵∠DCB=∠ABD=∠AOB=90°
∴∠DBC+ ∠CDB=90°,∠DBC+∠ABO=90°
∴∠CDB=∠ABO,
∴△DCB≌△BOA(AAS),
∴DC=OB=1,BC=OA=2
∴D(3,1)
设直线12的解析式为y=kx+b,则
![]() 解得
解得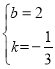
∴直线l2的函数表达式为y=![]() x+2
x+2
故答案为y=![]() x+2
x+2

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目