Question

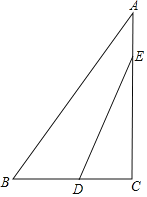
【题目】如图，菱形ABCD的顶点A，D在直线l上，∠BAD=60°，以点A为旋转中心将菱形ABCD顺时针旋转α（0°＜α＜30°），得到菱形AB′C′D′，B′C′交对角线AC于点M，C′D′交直线l于点N，连接MN，当MN∥B′D′ 时，解答下列问题：

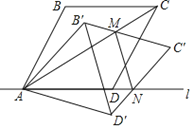
(1)求证：△AB′M≌△AD′N；

(2)求α的大小.

Answer 1

【答案】（1）见解析；（2）α=15°

【解析】

（1）利用四边形AB′C′D′是菱形，得到AB′=B′C′=C′D′=AD′，根据∠B′AD′=∠B′C′D′=60°，可得△AB′D′，△B′C′D′是等边三角形，进而得到△C′MN是等边三角形，则有C′M=C′N，MB′=ND′，利用SAS即可证明△AB′M≌△AD′N；

（2）由（1）得∠B′AM=∠D′AN，利用∠CAD=∠BAD=30°，即可解决问题.

（1）∵四边形AB′C′D′是菱形，

∴AB′=B′C′=C′D′=AD′，

∵∠B′AD′=∠B′C′D′=60°，

∴△AB′D′，△B′C′D′是等边三角形，

∵MN∥B′C′，

∴∠C′MN=∠C′B′D′=60°，∠CNM=∠C′D′B′=60°，

∴△C′MN是等边三角形，

∴C′M=C′N，

∴MB′=ND′，

∵∠AB′M=∠AD′N=120°，AB′=AD′，

∴△AB′M≌△AD′N（SAS），

（2）由△AB′M≌△AD′N得：∠B′AM=∠D′AN，

∵∠CAD=∠BAD=30°，

∴∠D′AN=∠B′AM=15°，

∴α=15°