题目内容
某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(单位:万元)与销售量x(单位:辆)之间分别满足: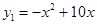 ,
,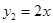 ,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为
,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为
| A.30万元 | B.40万元 | C.45万元 | D.46万元 |
D.
解析试题分析:设在甲地销售x辆,则在乙地销售(15-x)量,根据题意得出:
W=y1+y2=-x2+10x+2(15-x)=-x2+8x+30,
∴最大利润为: (万元),
(万元),
故选D.
考点:二次函数的应用.

练习册系列答案
相关题目
为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米) | 0.3 |
| 超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
| 超过m平方米部分 | 0.7 |
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.
已知关于 的一元二次方程
的一元二次方程 的两个实数根分别为
的两个实数根分别为 ,
, (
( ),则二次函数
),则二次函数 中,当
中,当 时,
时, 的取值范围是( )
的取值范围是( )
A. | B.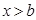 | C. | D. 或 或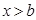 |
如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣ ;④3≤n≤4中,正确的是( )。
;④3≤n≤4中,正确的是( )。
| A.①② | B.③④ | C.①④ | D.①③ |
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;则其中说法正确的是( ).
| A.①② | B.②③ | C.①②④ | D.②③④ |
如图,正方形ABCD的边长为6cm,O是AB的中点,也是抛物线的顶点,OP⊥AB,两半圆的直径分别为OA,OB,抛物线经过C,D两点,且关于OP对称,则图中阴影部分的面积为( )(π取3.14,结果保留两位小数)
| A.7.07cm2 |
| B.3.53cm2 |
| C.14.13cm2 |
| D.10.60cm2 |
西宁中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3米,此时距喷水管的水平距离为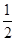 米,在如图所示的坐标系中,这个喷泉的函数关系式是( )
米,在如图所示的坐标系中,这个喷泉的函数关系式是( )
A.y=- +3 +3 | B.y=-3 +3 +3 |
C.y=-12 +3 +3 | D.y=-12 +3 +3 |
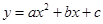 (
( )的图象如图所示,对称轴是直线
)的图象如图所示,对称轴是直线 ,有下列结论:①
,有下列结论:①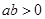 ;②
;② ;③
;③ ;④
;④ .其中正确结论的个数是( ).
.其中正确结论的个数是( ).



