题目内容
为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米) | 0.3 |
| 超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
| 超过m平方米部分 | 0.7 |
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.
(1)42(万元)
(2)由题意,得
①当0≤x≤30时,y=0.9x;
②当30<x≤m时,y=1.5x﹣18;
③当x>m时,∴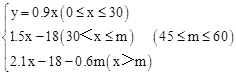 。
。
(3)45≤m<50
解析分析:(1)根据房款=房屋单价×购房面积就可以表示出应缴房款。
(2)由分段函数当0≤x≤30,当30<x≤m时,当x>m时,分别求出y与x之间的表达式即可。
(3)当50≤m≤60和当45≤m<50时,分别讨论建立不等式组就可以求出结论。
解:(1)由题意,得
三口之家应缴购房款为:0.3×90+0.5×30=42(万元)。
(2)由题意,得
①当0≤x≤30时,y=0.3×3x=0.9x;
②当30<x≤m时,y=0.9×30+0.5×3×(x﹣30)=1.5x﹣18;
③当x>m时,y=0.3×30+0.5×3(m﹣30)+0.7×3×(x﹣m)=2.1x﹣18﹣0.6m;
∴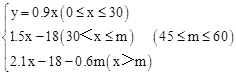 。
。
(3)由题意,得
①当50≤m≤60时,y=1.5×50﹣18=57(舍)。
②当45≤m<50时,y="2.1×50" 0.6m﹣18=87﹣0.6m,
∵57<y≤60,∴57<87﹣0.6m≤60,∴45≤m<50。
综合①②得45≤m<50。

某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
| | 甲 | 乙 |
| 进价(元/部) | 4000 | 2500 |
| 售价(元/部) | 4300 | 3000 |
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
抛物线y=﹣2x2经过平移到y=﹣2x2﹣4x﹣5,平移方法是( )
| A.向左平移1个单位,再向上平移3各单位 |
| B.向左平移1个单位,再向下平移3个单位 |
| C.向右平移1个单位,再向上平移3个单位 |
| D.向右平移1个单位,再向下平移3个单位 |
已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
| A.b≥-1 | B.b≤-1 | C.b≥1 | D.b≤1 |
某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(单位:万元)与销售量x(单位:辆)之间分别满足: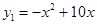 ,
,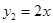 ,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为
,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为
| A.30万元 | B.40万元 | C.45万元 | D.46万元 |
 与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= .
.
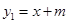 与
与 轴、
轴、 轴分别交于点
轴分别交于点 ,与双曲线
,与双曲线
 分别交于点
分别交于点 ,且
,且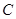 点的坐标为
点的坐标为 .
.
 及双曲线的解析式;
及双曲线的解析式; 的坐标;
的坐标; 在什么范围内取值时,
在什么范围内取值时,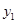 >
> .
. 与抛物线
与抛物线 的图象都经过
的图象都经过 轴上的D点,抛物线与
轴上的D点,抛物线与 轴交于A、B两点,其对称轴为直线
轴交于A、B两点,其对称轴为直线 ,且
,且 .直线
.直线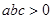 ; ②
; ② ; ③
; ③ ; ④
; ④ ; ⑤
; ⑤
