题目内容
已知二次函数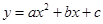 (
( )的图象如图所示,对称轴是直线
)的图象如图所示,对称轴是直线 ,有下列结论:①
,有下列结论:①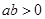 ;②
;② ;③
;③ ;④
;④ .其中正确结论的个数是( ).
.其中正确结论的个数是( ).
| A.1 | B.2 | C.3 | D.4 |
C.
解析试题分析:①∵- <0,∴ab>0,故①正确;
<0,∴ab>0,故①正确;
②∵x=1时,y<0,∴a+b+c<0,故②正确;
③∵- =-
=- ,∴2a=3b,又x=-1时,y>0,∴a-b+c>0,∴2a-2b+2c>0,∴3b-2b+2c>0,即b+2c>0,故③错误;
,∴2a=3b,又x=-1时,y>0,∴a-b+c>0,∴2a-2b+2c>0,∴3b-2b+2c>0,即b+2c>0,故③错误;
④∵抛物线开口向下,∴a<0,
∵ab>0,∴b<0,∴-2b>0(1).
∵抛物线交y轴于正半轴,∴c>0(2),
又∵a-b+c>0(3),
b+2c>0(4),
(1)+(2)+(3)+(4),得a-2b+4c>0,故④正确.
故选C.
考点:二次函数图象与系数的关系.

练习册系列答案
相关题目
将二次函数 化为
化为 的形式,下列结果正确的是[( )]
的形式,下列结果正确的是[( )]
A. | B.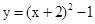 |
C. | D. |
某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(单位:万元)与销售量x(单位:辆)之间分别满足: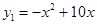 ,
,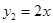 ,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为
,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为
| A.30万元 | B.40万元 | C.45万元 | D.46万元 |
关于二次函数y=2x2+3,下列说法中正确的是( )
| A.它的开口方向是向下 | B.当x<-1时,y随x的增大而减小 | C.它的顶点坐标是(2,3) | D.当x=0时,y有最大值是3 |
数形结合是数学中常用的思想方法,试运用这一思想方法确定函数y=x2+1与y= 的交点的横坐标x0的取值范围是( )
的交点的横坐标x0的取值范围是( )
| A.0<x0<1 |
| B.1<x0<2 |
| C.2<x0<3 |
| D.﹣1<x0<0 |
设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是________.
| A.c=3 | B.c≥3 | C.1≤c≤3 | D.c≤3 |
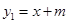 与
与 轴、
轴、 轴分别交于点
轴分别交于点 ,与双曲线
,与双曲线
 分别交于点
分别交于点 ,且
,且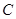 点的坐标为
点的坐标为 .
.
 及双曲线的解析式;
及双曲线的解析式; 的坐标;
的坐标; 在什么范围内取值时,
在什么范围内取值时,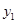 >
> .
. 的图象交点的横坐标,用此方法可推断方程x3+x-1=0的实数根x所在范围为( )
的图象交点的横坐标,用此方法可推断方程x3+x-1=0的实数根x所在范围为( )
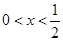


 向下平移2个单位,再向右平移1个单位,所得到的抛物线是( )
向下平移2个单位,再向右平移1个单位,所得到的抛物线是( )


