Question

【题目】在平面直角坐标系中，点，将点A向右平移6个单位长度，得到点B.

(1)直接写出点B的坐标；

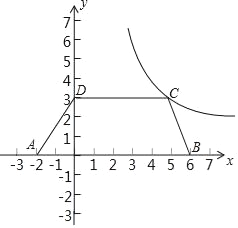
(2)若抛物线y=-x2+bx+c经过点A,B，求抛物线的表达式；

(3)若抛物线y=-x2+bx+c的顶点在直线y=x+2上移动，当抛物线与线段AB有且只有一个公共点时，求抛物线顶点横坐标的取值范围．

Answer 1

【答案】(1)；(2)抛物线表达式为；(3)或．

【解析】

（1）根据点的平移规律可得点B坐标；

（2）根据A、B两点坐标，利用待定系数法可求得解析式；

（3）由顶点在直线l上可设顶点坐标为（t，t+2），继而可得抛物线解析式为y＝﹣（x﹣t）2+t+2，根据抛物线与线段AB有一个公共点，考虑抛物线过点A或点B临界情况可得t的范围．

(1)根据平移的性质，可得：；

(2) ∵抛物线过点，∴，解得：，∴抛物线表达式为；

(3)∵抛物线顶点在直线上 ，∴抛物线顶点坐标为 ，∴抛物线表达式可化为．

把代入表达式可得：

解得：．

∴．

把代入表达式可得．

解得：

∴．

综上可知：的取值范围时或．