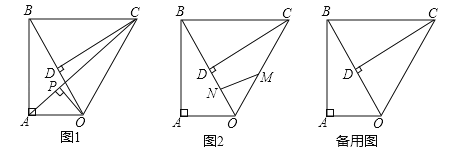
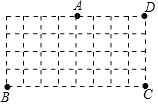
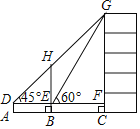
ΧβΡΩΡΎ»ί
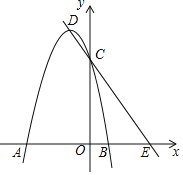
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§≈ΉΈοœΏy=ax2+2ax©¹3aΘ®aΘΦ0Θ©”κx÷αœύΫΜ”ΎAΘ§BΝΫΒψΘ§”κy÷αœύΫΜ”ΎΒψCΘ§ΕΞΒψΈΣDΘ§÷±œΏDC”κx÷αœύΫΜ”ΎΒψEΘ°
Θ®1Θ©Β±a=©¹1 ±Θ§«σ≈ΉΈοœΏΕΞΒψDΒΡΉχ±ξΘ§OEΒ»”ΎΕύ…ΌΘΜ
Θ®2Θ©OEΒΡ≥Λ «Ζώ”κa÷Β”–ΙΊΘ§ΥΒΟςΡψΒΡάμ”…ΘΜ
Θ®3Θ©…ηΓœDEO=Π¬Θ§45ΓψΓήΠ¬Γή60ΓψΘ§«σaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®4Θ©“‘DEΈΣ–±±ΏΘ§‘Ύ÷±œΏDEΒΡΉσœ¬ΖΫΉςΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈPDEΘ°…ηPΘ®mΘ§nΘ©Θ§÷±Ϋ”–¥≥ωnΙΊ”ΎmΒΡΚ· ΐΫβΈω ΫΦΑΉ‘±δΝΩmΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©Θ®©¹1Θ§4Θ©Θ§3ΘΜΘ®2Θ©Ϋα¬έΘΚOEΒΡ≥Λ”κa÷ΒΈόΙΊΘ°άμ”…ΦϊΫβΈωΘΜΘ®3Θ©©¹![]() ΓήaΓή©¹1ΘΜΘ®4Θ©n=©¹m©¹1Θ®mΘΦ1Θ©Θ°
ΓήaΓή©¹1ΘΜΘ®4Θ©n=©¹m©¹1Θ®mΘΦ1Θ©Θ°
ΓΨΫβΈωΓΩ
(1)«σ≥ω÷±œΏCDΒΡΫβΈω ΫΦ¥Ω…ΫβΨωΈ ΧβΘΜ
(2)άϊ”Ο≤Έ ΐaΘ§«σ≥ω÷±œΏCDΒΡΫβΈω Ϋ«σ≥ωΒψEΉχ±ξΦ¥Ω…≈–ΕœΘΜ
(3)«σ≥ω¬δ‘ΎΧΊ β«ι–Έœ¬ΒΡaΒΡ÷ΒΦ¥Ω…≈–ΕœΘΜ
(4)»γΆΦΘ§ΉςPMΓΆΕ‘≥Τ÷α”ΎMΘ§PNΓΆAB”ΎNΘ°ΝΫΧθ»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…ΫβΨωΈ Χβ.
ΫβΘΚ(1)Β±a=©¹1 ±Θ§≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=©¹x2©¹2x+3Θ§
ΓύΕΞΒψD(©¹1Θ§4)Θ§C(0Θ§3)Θ§
Γύ÷±œΏCDΒΡΫβΈω ΫΈΣy=©¹x+3Θ§
ΓύEΘ®3Θ§0Θ©Θ§
ΓύOE=3Θ§
(2)Ϋα¬έΘΚOEΒΡ≥Λ”κa÷ΒΈόΙΊΘ°
άμ”…ΘΚΓΏy=ax2+2ax©¹3aΘ§
ΓύC(0Θ§©¹3a)Θ§D(©¹1Θ§©¹4a)Θ§
Γύ÷±œΏCDΒΡΫβΈω ΫΈΣy=ax©¹3aΘ§
Β±y=0 ±Θ§x=3Θ§
ΓύEΘ®3Θ§0Θ©Θ§
ΓύOE=3Θ§
ΓύOEΒΡ≥Λ”κa÷ΒΈόΙΊΘ°
(3)Β±Π¬=45Γψ ±Θ§OC=OE=3Θ§
Γύ©¹3a=3Θ§
Γύa=©¹1Θ§
Β±Π¬=60Γψ ±Θ§‘ΎRtΓςOCE÷–Θ§OC=![]() OE=3
OE=3![]() Θ§
Θ§
Γύ©¹3a=3![]() Θ§
Θ§
Γύa=©¹![]() Θ§
Θ§
Γύ45ΓψΓήΠ¬Γή60ΓψΘ§aΒΡ»Γ÷ΒΖΕΈßΈΣ©¹![]() ΓήaΓή©¹1Θ°
ΓήaΓή©¹1Θ°
(4)»γΆΦΘ§ΉςPMΓΆΕ‘≥Τ÷α”ΎMΘ§PNΓΆAB”ΎNΘ°

ΓΏPD=PEΘ§ΓœPMD=ΓœPNE=90ΓψΘ§ΓœDPE=ΓœMPN=90ΓψΘ§
ΓύΓœDPM=ΓœEPNΘ§
ΓύΓςDPMΓ’ΓςEPNΘ§
ΓύPM=PNΘ§PM=ENΘ§
ΓΏD(©¹1Θ§©¹4a)Θ§E(3Θ§0)Θ§
ΓύEN=4+n=3©¹mΘ§
Γύn=©¹m©¹1Θ§
Β±ΕΞΒψD‘Ύx÷α…œ ±Θ§P(1Θ§©¹2)Θ§¥Υ ±mΒΡ÷Β1Θ§
ΓΏ≈ΉΈοœΏΒΡΕΞΒψ‘ΎΒΎΕΰœσœόΘ§
ΓύmΘΦ1Θ°
Γύn=©¹m©¹1(mΘΦ1)Θ°
Ι ¥πΑΗΈΣΘΚ(1)(©¹1Θ§4)Θ§3ΘΜ(2)OEΒΡ≥Λ”κa÷ΒΈόΙΊΘΜ(3)©¹![]() ΓήaΓή©¹1ΘΜ(4)n=©¹m©¹1Θ®mΘΦ1Θ©Θ°
ΓήaΓή©¹1ΘΜ(4)n=©¹m©¹1Θ®mΘΦ1Θ©Θ°

 –«ΦΕΩΎΥψΧλΧλΝΖœΒΝ–¥πΑΗ
–«ΦΕΩΎΥψΧλΧλΝΖœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΘ®9Ζ÷Θ©Ψ≈ΡξΦΕ ΐ―ß–Υ»Λ–ΓΉιΨ≠Ιΐ –≥ΓΒς≤ιΘ§ΒΟΒΫΡ≥÷÷‘ΥΕ·ΖΰΟΩ‘¬ΒΡœζΝΩ”κ έΦέΒΡœύΙΊ–≈œΔ»γœ¬±μΘΚ
έΦέΘ®‘Σ/ΦΰΘ© | 100 | 110 | 120 | 130 | Γ≠ |
‘¬œζΝΩΘ®ΦΰΘ© | 200 | 180 | 160 | 140 | Γ≠ |
“―÷ΣΗΟ‘ΥΕ·ΖΰΒΡΫχΦέΈΣΟΩΦΰ60‘ΣΘ§…η έΦέΈΣ![]() ‘ΣΘ°
‘ΣΘ°
Θ®1Θ©«κ”ΟΚ§xΒΡ ΫΉ”±μ ΨΘΚΔΌœζ έΗΟ‘ΥΕ·ΖΰΟΩΦΰΒΡάϊ»σ « ‘ΣΘΜΔΎ‘¬œζΝΩ « ΦΰΘΜΘ®÷±Ϋ”–¥≥ωΫαΙϊΘ©
Θ®2Θ©…ηœζ έΗΟ‘ΥΕ·ΖΰΒΡ‘¬άϊ»σΈΣ![]() ‘ΣΘ§Ρ«Ο¥ έΦέΈΣΕύ…Ό ±Θ§Β±‘¬ΒΡάϊ»σΉν¥σΘ§Ήν¥σάϊ»σ «Εύ…ΌΘΩ
‘ΣΘ§Ρ«Ο¥ έΦέΈΣΕύ…Ό ±Θ§Β±‘¬ΒΡάϊ»σΉν¥σΘ§Ήν¥σάϊ»σ «Εύ…ΌΘΩ