Question

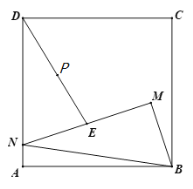
【题目】如图，M为正方形ABCD内一点，点N在AD边上，且∠BMN＝90°，MN＝2MB．点E为MN的中点，点P为DE的中点，连接MP并延长到点F，使得PF＝PM，连接DF．

（1）依题意补全图形；

（2）求证：DF＝BM；

（3）连接AM，用等式表示线段PM和AM的数量关系并证明．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）,证明见解析.

【解析】

（1）图见详解,

（2）证明△MPE≌△FPD（SAS）得DF＝ME,由E为MN的中点得MN＝2ME,MN＝2MB,等量代换即可解题,

（3）证明△FAD≌△MAB（SAS）,推出△FAM为等腰直角三角形,即可证明结论.

解：（1）

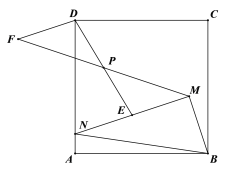
（2）∵点P为线段DE的中点

∴DP＝EP

在△MPE和△FPD中

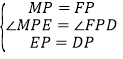
∴△MPE≌△FPD（SAS）

∴DF＝ME

∵E为MN的中点

∴MN＝2ME

∵MN＝2MB

∴MB＝ME＝DF，∴DF＝BM

（3）结论：

连接AF

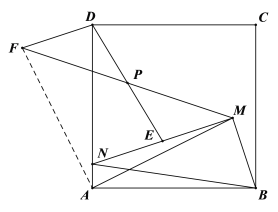
由（2）可知：△MPE≌△FPD

∴∠DFP＝∠EMP.

∴DF∥ME.

∴∠FDN＝∠MND.

在正方形ABCD中，AD＝AB，∠BAD＝90°

又∵∠BMN＝90°

∴∠MBA＋∠MNA＝180°

又∵∠MNA＋∠MND＝180°

∴∠MBA＝∠MND

∴∠FDN＝∠MBA

在△FAD和△MAB中

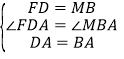
∴△FAD≌△MAB（SAS）

∴∠FAD＝∠MAB,FA＝MA

∴∠FAM＝∠DAB＝90°

∴△FAM为等腰直角三角形

∴

又∵FM＝2PM

∴