Question

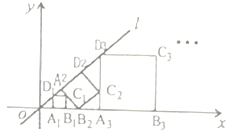
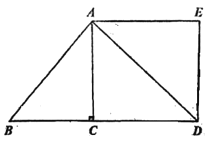
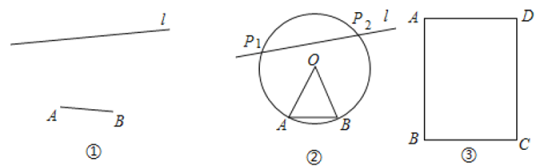
【题目】如图①，已知线段和直线，用直尺和圆规在上作出所有的点，使得，如图②，小明的作图方法如下：

第一步：分别以点，为圆心，长为半径作弧，两弧在上方交于点；

第二步：连接，；

第三步：以为圆心，长为半径作，交于，；

所以图中，即为所求的点.

（1）在图②中，连接，，说明；

（方法迁移）

（2）如图③，用直尺和圆规在矩形内作出所有的点，使得（不写作法，保留作图痕迹）.

（深入探究）

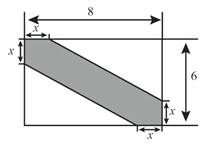
（3）已知矩形，，，为边上的点，若满足的点恰有两个，求的取值范围.

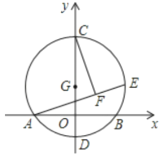
（4）已知矩形，，，为矩形内一点，且，若点绕点逆时针旋转到点，求的最小值.

Answer 1

【答案】（1）见解析；（2）见解析；（3）2≤m＜+1；（4）．

【解析】

（1）先根据等边三角形得：∠AOB=60°，则根据圆周角定理可得：∠AP1B=30°；
（2）先作等腰直角三角形BEC、BFC，再作△EBC的外接圆，可得圆心角∠BOC=90°，则弧BC所对的圆周角都是45°；
（3）先确定⊙O，根据同弧所对的圆周角相等可得AD在四边形GEFH内部时符合条件；
（4）先确定⊙O，根据圆周角定理正确画出∠BPC=135°，利用勾股定理求OF的长，知道A、P、O在同一直线上时，AP最小，则PQ的值最小，求AE的长，即是AP的长，可得PQ的最小值．

解：（1）∵OA=OB=AB，
∴△OAB是等边三角形，
∴∠AOB=60°，
由题意得：∠AP1B=∠AOB=30°；
（2）如图，①以B、C为圆心，以BC为半径作圆，交AB、DC于E、F，

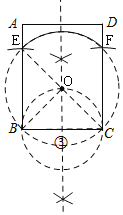
②作BC的中垂线，连接EC，交于O，
③以O为圆心，OE为半径作圆，
则弧EF上所有的点（不包括E、F两点）即为所求；
（3）如图④，同理作⊙O，

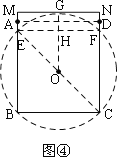
∵BE=BC=2，
∴CE=2，
∴⊙O的半径为，即OE=OG=，
∵OG⊥EF，
∴EH=1，
∴OH=1，
∴GH=-1，
∴BE≤AB＜MB，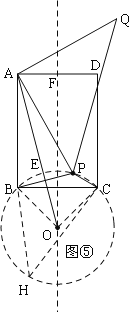
∴2≤m＜2+-1，即2≤m＜+1，
故答案为：2≤m＜+1；
（4）如图⑤，构建⊙O，使∠COB=90°，在弧BC上取一点H，则∠CHB=45°
∴∠CPB=135°，
由旋转得：△APQ是等腰直角三角形，
∴PQ=AP，
∴PQ取最小值时，就是AP取最小值，
当P与E重合时，即A、P、O在同一直线上时，AP最小，则PQ的值最小，
在Rt△AFO中，AF=1，OF=3+1=4，
∴AO=，
∴AE==AP，
∴PQ=AP=（）=．
故答案为：．