题目内容
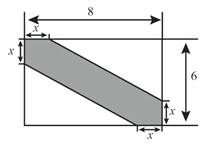
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
【答案】(1)y= x2-14x+48(0<x<6);(2)1;(3)改造后剩余油菜花地所占面积的最大值为41.25m2.
【解析】分析:(1)、利用三角形的面积计算公式得出y与x的函数关系式;(2)、将y=35代入函数解析式求出x的值;(3)、利用配方法将函数配成顶点式,然后根据函数的增减性得出最值.
详解:解:(1)、y=2×![]() (8-x)(6-x)=x2-14x+48.
(8-x)(6-x)=x2-14x+48.
(2)、由题意,得 x2-14x+48=6×8-13, 解得:x1=1,x2=13(舍去). 所以x=1.
(3)、y=x2-14x+48=(x-7)2-1.
因为a=1>0,所以函数图像开口向上,当x<7时,y随x的增大而减小.
所以当x=0.5时,y最大.最大值为41.25.
答:改造后油菜花地所占面积的最大值为41.25 m2.

练习册系列答案
相关题目