��Ŀ����
��ֱ������ϵ���к���y=
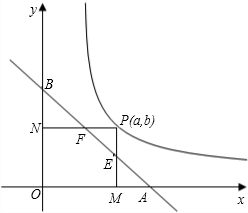
��x��0����һ��ֱ�ߵ�ͼ��ֱ����x��y��������ֱ��ڵ�A�͵�B����OA=OB=1����PΪ����������һ�㣬���������ǣ�a��b�����ɵ�P��x�ᡢy��������PM��PN��M��NΪ���㣩�ֱ���ֱ��AB�ཻ�ڵ�E�͵�F��
��1���������E��F�����߶�AB�ϣ���ͼ�����ֱ����E��F������ֻ꣨��д���𰸣�����д��������̣���
��2������P���������ƶ��������OEF��������������a��b�Ĵ���ʽ��ʾ����
��3�����AF=
����
��ֵ��
| 1 |
| 2x |
��1���������E��F�����߶�AB�ϣ���ͼ�����ֱ����E��F������ֻ꣨��д���𰸣�����д��������̣���
��2������P���������ƶ��������OEF��������������a��b�Ĵ���ʽ��ʾ����
��3�����AF=
| ||
| 2 |
| OF |
| OE |

��1����E��a��1-a������F��1-b��b����

��2��S��EOF=S����MONP-S��EMO-S��FNO-S��EPF��
=ab-
a(1-a)-
b(1-b)-
(a+b-1)2��
=
(a+b-1)��
��3����AF=
��F��1-b��b��
��2b2=(
)2
��b=
��
=
a=
�ɵ�F�͵�E�����������ã�
OF=
��OE=
��
��
=
��

��2��S��EOF=S����MONP-S��EMO-S��FNO-S��EPF��
=ab-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
��3����AF=
| ||
| 2 |
��2b2=(
| ||
| 2 |
��b=
| ||
| 2 |
��
| ||
| 2 |
| 1 |
| 2a |
a=
| ||
| 3 |
�ɵ�F�͵�E�����������ã�
OF=
| ||
| 2 |
| ||||
| 3 |
��
| OF |
| OE |
3
| ||||
30-4
|

��ϰ��ϵ�д�
 ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
�����Ŀ