题目内容
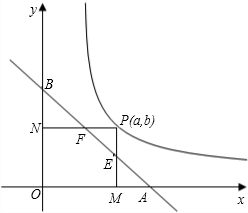
如图,反比例函数y=
(x>0)的图象经过边长为3的正方形OABC的顶点B,点P(m,n)为该函数图象上的一动点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,设矩形OEPF和正方形OABC不重合部分的面积为S(即图中阴影部分的面积).
(1)求k的值;
(2)当m=4时,求n和S的值;
(3)求S关于m的函数解析式.

| k |
| x |
(1)求k的值;
(2)当m=4时,求n和S的值;
(3)求S关于m的函数解析式.

(1)由题意可知点B的坐标为:(3,3),将其代入y=
中,得:
3=
,
解得:k=9;
(2)由(1)知反比例函数的解析式为y=
,把(4,n)代入,得n=
,
如图1,
则S=S矩形BCFN+S矩形AEPN=3×(3-
)+(4-3)×
=4.5;
(3)分两种情况:
∵点P(m,n)为该函数y=
图象上的一动点,
∴n=
,
如图2,
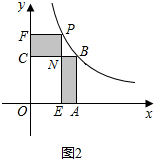
当0<m<3时,S=S矩形PFCN+S矩形BNEA
=PF•FC+AB•BN
=m(
-3)+3×(3-m)
=18-6m,
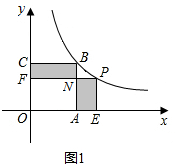
如图1,当m>3时,S=S矩形BCFN+S矩形AEPN
=BC•BN+PE•AE
=3×(3-
)+
(m-3)
=18-
.
| k |
| x |
3=
| k |
| 3 |
解得:k=9;
(2)由(1)知反比例函数的解析式为y=
| 9 |
| x |
| 9 |
| 4 |
如图1,

则S=S矩形BCFN+S矩形AEPN=3×(3-
| 9 |
| 4 |
| 9 |
| 4 |
(3)分两种情况:
∵点P(m,n)为该函数y=
| 9 |
| x |
∴n=
| 9 |
| m |
如图2,

当0<m<3时,S=S矩形PFCN+S矩形BNEA
=PF•FC+AB•BN
=m(
| 9 |
| m |
=18-6m,
如图1,当m>3时,S=S矩形BCFN+S矩形AEPN
=BC•BN+PE•AE
=3×(3-
| 9 |
| m |
| 9 |
| m |
=18-
| 54 |
| m |

练习册系列答案
相关题目