题目内容
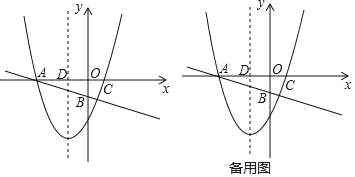
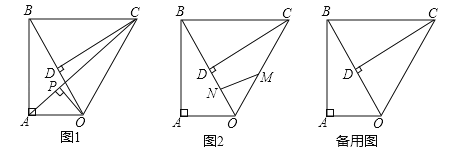
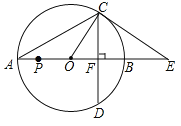
【题目】如图,以AB为直径的⊙O与CE相切于点C,CE交AB的延长线于点E,直径AB=18,∠A=30°,弦CD⊥AB,垂足为点F,连接AC,OC,则下列结论正确的是______.(写出所有正确结论的序号)
①![]() ;
;
②扇形OBC的面积为![]() π;
π;
③△OCF∽△OEC;
④若点P为线段OA上一动点,则APOP有最大值20.25.
【答案】①③④.
【解析】
利用垂径定理对①进行判断;利用圆周角定理得到∠BOC=2∠A=60°,则利用扇形的面积公式可计算出扇形OBC的面积,于是可对②进行判断;利用切线的性质得到OC⊥CE,然后根据相似三角形的判定方法对③进行判断;由于APOP=-(OP-![]() )2+
)2+![]() ,则可利用二次函数的性质对④进行判断.
,则可利用二次函数的性质对④进行判断.
∵弦CD⊥AB,AB是直径,
∴![]() ,所以①正确;
,所以①正确;
∴∠BOC=2∠A=2×30°=60°,
∴扇形OBC的面积=![]() ,所以②错误;
,所以②错误;
∵⊙O与CE相切于点C,
∴OC⊥CE,
∴∠OCE=90°,
∵∠COF=∠EOC,∠OFC=∠OCE,
∴△OCF∽△OEC,所以③正确;
∵APOP=(9-OP)OP= -(OP-![]() )2+
)2+![]() ,
,
当OP=![]() 时,APOP的最大值为
时,APOP的最大值为![]() =20.25,所以④正确,
=20.25,所以④正确,
故答案为:①③④.

练习册系列答案
相关题目