题目内容
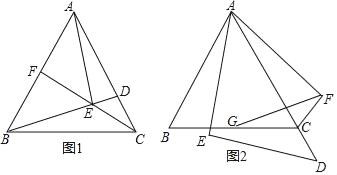
【题目】如图,在等边△ABC中,点D是AC边上一点,连接BD,过点A作AE⊥BD于E.
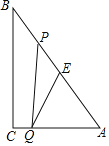
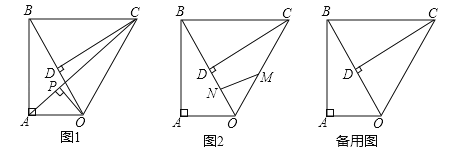
(1)如图1,连接CE并延长CE交AB于点F,若∠CBD=15°,AB=4,求CE的长;
(2)如图2,当点D在线段AC的延长线上时,将线段AE绕点A逆时针旋转60°得到线段AF,连接EF,交BC于G,连接CF,求证:BG=CG.
【答案】(1)2![]() -2(2)证明见解析
-2(2)证明见解析
【解析】
先证明∠BAE=∠ABE=45°,结合AC=BC可证CF垂直平分AB,从而可求出AF=BF=EF=2,由勾股定理求出CF的长,即可求出CE的长;
(2)过点C作CM∥BD,由旋转的性质可证△AEF为等边三角形,然后通过证明△ABE≌△ACF和△BGE≌△GMC可证明结论成立.
(1)∵△ABC为等边三角形,
∴AB=BC=AC=4,∠BAC=60°且∠DBC=15°,
∴∠ABE=45°且AE⊥BD,
∴∠BAE=∠ABE=45°,
∴AE=BE,且AC=BC
∴CF垂直平分AB,即AF=BF=2,CF⊥AB.
∵∠ABE=45°,
∴∠FEB=∠ABE=45°,
∴BF=EF=2,
∵Rt△BCF中,
CF=![]() =2
=2![]() ,
,
∴CE=2![]() ﹣2;
﹣2;
(2)如图2:过点C作CM∥BD,
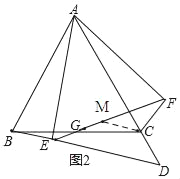
∵将线段AE绕点A逆时针旋转60°得到线段AF
∴AE=AF,∠EAF=60°,
∴△AEF为等边三角形,
∴∠AFE=∠AEF=60°,
∴∠FAC+∠EAC=60°,且∠BAE+∠EAC=60°,
∴∠BAE=∠CAF,且AB=AC,AE=AF,
∴△ABE≌△ACF,
∴BE=CF,∠AEB=∠AFC=90°,
∴∠BEF=150°,∠MFC=30°.
∵MC∥BD,
∴∠BEF=∠GMC=150°,
∴∠CMF=30°=∠CFM,
∴CM=CF且CF=BE,
∴BE=CM且∠BGE=∠CGM,∠BEG=∠CMG,
∴△BGE≌△GMC,
∴BG=GC.

 名校课堂系列答案
名校课堂系列答案