题目内容
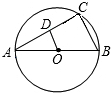
如图,点D、C是以AB为直径的半圆上的两点,O为圆心,DE与AC相交于点E,OC∥AD,AB=5,cos∠CAB=0.8,求CE和DE的长.


解:OC交BD于F点,连结BC,如图,
∵AB为直径,
∴∠D=90°,∠ACB=90°,
∵cos∠CAB=
=0.8,AB=5,
∴AC=4,
∴BC=
=3,
∵OC∥AD,
∴∠OFB=90°,即OF⊥DB,
∴DC弧=BC弧,DF=BF,
∴∠CBD=∠CAB,
在Rt△CBF中,cos∠CBF=0.8=
,则BF=2.4,
∴CF=
=1.8,
在Rt△CEF中,∠ECF=∠CAB,
∴cos∠ECF=0.8=
,
∴EC=
=
,
∴EF=
=
,
∵DE+EF=BF,
∴DE=2.4-
=1.05.

∵AB为直径,
∴∠D=90°,∠ACB=90°,
∵cos∠CAB=
| AC |
| AB |
∴AC=4,
∴BC=
| AB2-AC2 |
∵OC∥AD,
∴∠OFB=90°,即OF⊥DB,
∴DC弧=BC弧,DF=BF,
∴∠CBD=∠CAB,
在Rt△CBF中,cos∠CBF=0.8=
| BF |
| BC |
∴CF=
| BC2-BF2 |
在Rt△CEF中,∠ECF=∠CAB,
∴cos∠ECF=0.8=
| CF |
| EC |
∴EC=
| 1.8 |
| 0.8 |
| 9 |
| 4 |
∴EF=
| EC2-CF2 |
| 27 |
| 20 |
∵DE+EF=BF,
∴DE=2.4-
| 27 |
| 20 |


练习册系列答案
相关题目