题目内容
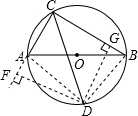
如图,AB是⊙O的直径,弦AC,BC的长分别为6和8,∠ACB的平分线交⊙O于D,则CD的长为( )

A.7
| B.8
| C.7 | D.9 |

过点D作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,
=
,
∴DA=DB.
∵∠AFD=∠BGD=90°,
在Rt△ADF和Rt△BDG,
,
∴Rt△AFD≌Rt△BGD(HL),
∴AF=BG.
同理:Rt△CDF≌Rt△CDG(HL),
∴CF=CG.
∵AC=6,BC=8,
∴6+AF=8-AF,
∴AF=1,CF=7,
∵AB是直径,
∴∠ACB=90°,
∴∠ACD=45°,
∵△CDF是等腰直角三角形,
∴CD=7
.
故选A.
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,
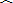 |
| AD |
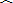 |
| BD |
∴DA=DB.
∵∠AFD=∠BGD=90°,
在Rt△ADF和Rt△BDG,
|
∴Rt△AFD≌Rt△BGD(HL),
∴AF=BG.
同理:Rt△CDF≌Rt△CDG(HL),
∴CF=CG.
∵AC=6,BC=8,
∴6+AF=8-AF,
∴AF=1,CF=7,
∵AB是直径,
∴∠ACB=90°,
∴∠ACD=45°,
∵△CDF是等腰直角三角形,
∴CD=7
| 2 |
故选A.


练习册系列答案
相关题目
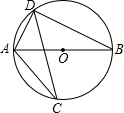



 点,连接FE,FG.
点,连接FE,FG.

