Question

【题目】如图，Rt△OAB的直角边OA在x轴上，顶点B的坐标为（6，8），直线CD交AB于点D（6，3），交x轴于点C（12，0）．

（1）求直线CD的函数表达式；

（2）动点P在x轴上从点（﹣10，0）出发，以每秒1个单位的速度向x轴正方向运动，过点P作直线l垂直于x轴，设运动时间为t．

①点P在运动过程中，是否存在某个位置，使得∠PDA=∠B？若存在，请求出点P的坐标；若不存在，请说明理由；

②请探索当t为何值时，在直线l上存在点M，在直线CD上存在点Q，使得以OB为一边，O，B，M，Q为顶点的四边形为菱形，并求出此时t的值．

Answer 1

【答案】（1）直线CD的解析式为y=﹣x+6；（2）①满足条件的点P坐标为（，0）或（，0）．②满足条件的t的值为或．

【解析】

（1）利用待定系数法即可解决问题；

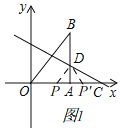
（2）①如图1中，作DP∥OB，则∠PDA=∠B．利用平行线分线段成比例定理，计算即可，再根据对称性求出P′；

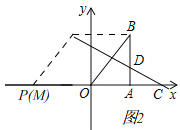
②分两种情形分别求解即可解决问题：如图2中，当OP=OB=10时，作PQ∥OB交CD于Q．如图3中，当OQ=OB时，设Q（m，﹣m+6），构建方程求出点Q坐标即可解决问题；

（1）设直线CD的解析式为y=kx+b，则有

，

解得，

∴直线CD的解析式为y=﹣x+6．

（2）①如图1中，作DP∥OB，则∠PDA=∠B．

∵DP∥OB，

∴，

∴，

∴，

∴OP=6﹣，

∴P（，0），

根据对称性可知，当AP=AP′时，P′（，0），

∴满足条件的点P坐标为（，0）或（，0）．

②如图2中，当OP=OB=10时，作PQ∥OB交CD于Q．

∵直线OB的解析式为y=x，

∴直线PQ的解析式为y=x+，

由，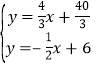

解得，

∴Q（﹣4，8），

∴PQ==10，

∴PQ=OB．

∵PQ∥OB，

∴四边形OBQP是平行四边形．

∵OB=OP，

∴四边形OBQP是菱形，此时点M与的Q重合，满足条件，t=0．

如图3中，当OQ=OB时，设Q（m，﹣m+6），

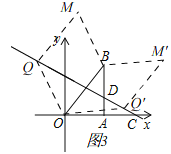
则有m2+（﹣m+6）2=102，解得m=，

∴点Q 的横坐标为或，

设点M的横坐标为a，则有：或，

∴a=或，

∴满足条件的t的值为或．