题目内容
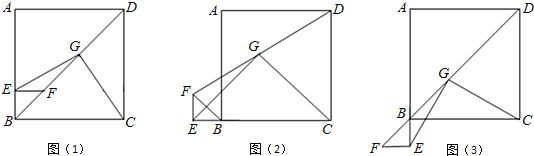
【题目】如图,将直角三角形ABC沿着斜边AC的方向平移到△DEF的位置(A、D. C. F四点在同一条直线上).直角边DE交BC于点G.如果BG=4,EF=12,△BEG的面积等于4,那么梯形ABGD的面积是( )
A.16B.20C.24D.28
【答案】B
【解析】
通过图可知梯形ABGD的面积=△ABC的面积-△CDG的面积=△DEF的面积-△CDG的面积=梯形EGCF的面积．
∵△DEF的是直角三角形ABC沿着斜边AC的方向平移后得到的，且A. D. C. F四点在同一条直线上，
∴BE∥AC，BC=EF，
∵BG=4，EF=12，
∴CG=BCBG=EFBG=124=8.
∵△BEG的面积等于4，
∴
BGGE=4，
∴GE=2，
∴梯形EGCF的面积= (CG+EF)GE= (8+12)×2=20，
∴梯形ABGD的面积=梯形EGCF的面积=20.
故选B.
练习册系列答案
名校通行证有效作业系列答案
相关题目
