��Ŀ����
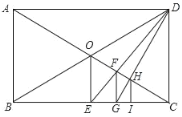
����Ŀ����ͼ���ı���ABCD�����Σ���BAD��120������E������AC�ϣ���������A�͵�C��������E��ֱ��GH��ֱ��AD�ڵ�G����ֱ��BC�ڵ�H����GH��DC����F��BC���ӳ����ϣ�CF��AG������ED��EF��DF��
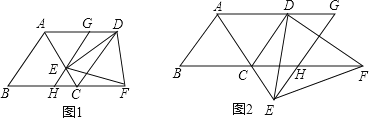
��1����ͼ1������E���߶�AC��ʱ��
���ж���AEG����״����˵�����ɣ�
����֤����DEF�ǵȱ������Σ�
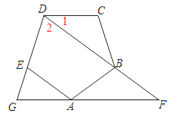
��2����ͼ2������E��AC���ӳ�����ʱ����DEF�ǵȱ�������������ǣ���֤����Ľ��ۣ�������ǣ���˵�����ɣ�
���𰸡���1������AEG�ǵȱ������Σ����ɼ���������֤������������2����DEF�ǵȱ������Σ����ɼ�������
��������
��1���������ε����ʵó�AD��BC��AB��BC��CD��AD��AB��CD����CAD��![]() ��BAD��60������ƽ���ߵ����ʵó���BAD����ADC��180������ADC��60������AGE����ADC��60�����ó���AGE����EAG����AEG��60�������ɵó���AEG�ǵȱ������Σ�
��BAD��60������ƽ���ߵ����ʵó���BAD����ADC��180������ADC��60������AGE����ADC��60�����ó���AGE����EAG����AEG��60�������ɵó���AEG�ǵȱ������Σ�
���ɵȱ������ε����ʵó�AG��AE������֪�ó�AE��CF�������ε����ʵó���BCD����BAD��120�����ó���DCF��60������CAD��֤����AED�ա�CFD��SAS�����ó�DE��DF����ADE����CDF����֤����EDF��60�������ɵó���DEF�ǵȱ������Σ�
��2��ͬ��1���ٵã���AEG�ǵȱ������Σ��ó�AG��AE������֪�ó�AE��CF�������ε����ʵó���BCD����BAD��120������CAD��![]() ��BAD��60�����ó���FCD��60������CAD��֤����AED�ա�CFD��SAS�����ó�DE��DF����ADE����CDF����֤����EDF��60�������ɵó���DEF�ǵȱ������Σ�
��BAD��60�����ó���FCD��60������CAD��֤����AED�ա�CFD��SAS�����ó�DE��DF����ADE����CDF����֤����EDF��60�������ɵó���DEF�ǵȱ������Σ�
��1�����⣺��AEG�ǵȱ������Σ��������£�
���ı���ABCD�����Σ���BAD��120����
��AD��BC��AB��BC��CD��AD��AB��CD����CAD��![]() ��BAD��60����
��BAD��60����
���BAD+��ADC��180����
���ADC��60����
��GH��DC��
���AGE����ADC��60����
���AGE����EAG����AEG��60����
���AEG�ǵȱ������Σ�
��֤�����ߡ�AEG�ǵȱ������Σ�
��AG��AE��
��CF��AG��
��AE��CF��
���ı���ABCD�����Σ�
���BCD����BAD��120����
���DCF��60������CAD��
����AED����CFD�� ��
��
���AED�ա�CFD��SAS��
��DE��DF����ADE����CDF��
�ߡ�ADC����ADE+��CDE��60����
���CDF+��CDE��60����
����EDF��60����
���DEF�ǵȱ������Σ�
��2���⣺��DEF�ǵȱ������Σ��������£�
ͬ��1�����ã���AEG�ǵȱ������Σ�
��AG��AE��
��CF��AG��
��AE��CF��
���ı���ABCD�����Σ�
���BCD����BAD��120������CAD��![]() ��BAD��60����
��BAD��60����
���FCD��60������CAD��
����AED����CFD�� ��
��
���AED�ա�CFD��SAS����
��DE��DF����ADE����CDF��
�ߡ�ADC����ADE����CDE��60����
���CDF����CDE��60����
����EDF��60����
���DEF�ǵȱ������Σ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�