题目内容
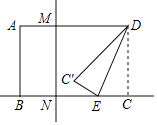
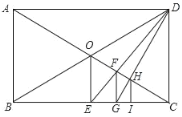
【题目】如图所示,在矩形ABCD中,对角线AC,BD相交于点O.
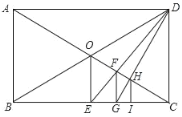
(1)过点O作OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于G点,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出位似比;若不是,请说明理由.
(2)连接DG交AC于点H,作HI⊥BC于I,试确定![]() 的值.
的值.
【答案】(1)是位似图形,位似中心是点C,位似比为3;(2)![]() .
.
【解析】
(1)根据相似三角形的判定定理证明△ABC∽△FGC,根据位似变换的概念和位似中心的概念解答即可,根据相似三角形的性质求出两个三角形的相似比,得到位似比;
(2)根据相似三角形的性质进行计算即可.
(1)∵FG⊥BC,AB⊥BC,
∴FG∥AB,
∴△ABC∽△FGC,
∵△ABC与△FGC对应顶点的连线相交于一点,对应边互相平行或重合,
∴△ABC与△FGC是位似图形,位似中心是点C,
∵BO=OD,OE∥CD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
则△ABC与△FGC的位似比为3;
(2)由(1)得,![]() ,FG∥CD,
,FG∥CD,
∴![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目