题目内容
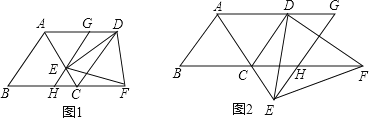
【题目】如图,在![]() 中,
中,![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,过点
,过点![]() 作
作![]() ,过
,过![]() 作
作![]() ,得阴影
,得阴影![]() ;再过
;再过![]() 作
作![]() ,过
,过![]() 作
作![]() ,得阴影
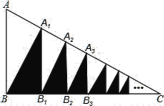
,得阴影![]() ;…如此下去,请猜测这样得到的所有阴影三角形的面积之和为( )
;…如此下去,请猜测这样得到的所有阴影三角形的面积之和为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
可从整体的角度来求解此题:易知所有白色部分的小直角三角形都与对应阴影部分的三角形相似,那么它们的面积比应该等于相似比的平方,它们的相似比为AB:A 1 B,而AB的长已知,只要求得A1B的长即可求得阴影部分占△ABC面积的比例大小,从而可求得阴影部分的面积和.
解:∵A1B1∥AB,∴∠ABA1=∠BA1B1,
∵∠AA1B=∠A1B1B=90°,∴Rt△ABA1 ∽△BA1B1,
同理可证:Rt△A1B1A2 ∽Rt△B1A2B2 ,
……;
即白色部分的小直角三角形与阴影部分的小直角三角形逐一对应相似,
在Rt△ABC中,BA1 ⊥AC,由S=![]() ABBC=
ABBC=![]() ACBA1,得BA1 =
ACBA1,得BA1 =![]() ,
,
∴AB:BA1 =3:![]() =5:4,
=5:4,
∴白色部分小直角三角形的面积和:阴影部分小直角三角形的面积和=AB2 :BA12 =25:16,
故S 阴影部分小直角三角形的面积和=![]() S△ABC=
S△ABC=![]() .故选D.
.故选D.

练习册系列答案
相关题目