题目内容
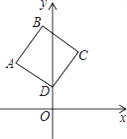
【题目】如图,在正方形ABCD中,点D的坐标为(0,1),点A的坐标是(﹣2,2),则点B的坐标为________.
【答案】(﹣1,4)
【解析】分析:过点A作AF⊥y轴,垂足为F,过点B作BE⊥AF,垂足为E.先证明△ABE≌△DAF,由全等三角形的性质可知DF=AE=1,AF=BE=2,于是可得到点B的坐标.
详解:如图所示:过点A作AF⊥y轴,垂足为F,过点B作BE⊥AF,垂足为E.
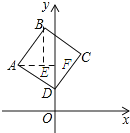
∵点D的坐标为(0,1),点A的坐标是(-2,2),
∴DF=1,AF=2.
∵四边形ABCD为正方形,
∴∠BAD=90°,AB=AD.
∵∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,
∴∠BAE=∠ADF.
∵在△ABE和△DAF中
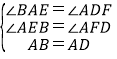 ,
,
∴△ABE≌△DAF.
∴DF=AE=1,AF=BE=2
∴EF=2-1=1,OF+BE=4.
∴B(-1,4).
故答案为:(-1,4).

练习册系列答案
相关题目