题目内容
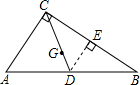
已知在△ABC中，∠C=90°，BC=8，AB=10，点G为重心，那么tan∠GCB的值为______．
如图，连接CG并延长交AB于点D，
∵点G为重心，
∴CD是△ABC的中线，
∴CD=BD=
AB=
×10=5，
过点D作DE⊥BC于点E，
则CE=BE=
BC=
×8=4，
在Rt△CDE中，DE=
=
=3，
∴tan∠GCB=
=
．
故答案为：
．
∵点G为重心，
∴CD是△ABC的中线，
∴CD=BD=
| 1 |
| 2 |
| 1 |
| 2 |
过点D作DE⊥BC于点E，
则CE=BE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△CDE中，DE=
| CD2-CE2 |
| 52-42 |
∴tan∠GCB=
| DE |
| CE |
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
练习册系列答案
导学教程高中新课标系列答案
相关题目
