题目内容
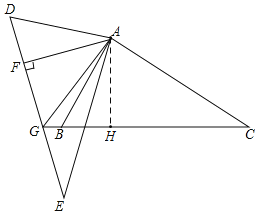
【题目】如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG,若S四边形DGBA=6,AF=![]() ,则FG的长是_____.
,则FG的长是_____.

【答案】4.
【解析】
过点A作AH⊥BC于H,可证明△ABC≌△ADE,得出AF=AH,再判定Rt△AFG≌Rt△AHG,即可得出![]() ,再判定Rt△ADF≌Rt△ABH,得出S四边形DGBA=S四边形AFGH=6,最后根据Rt△AFG的面积=3,进而得出FG的长.
,再判定Rt△ADF≌Rt△ABH,得出S四边形DGBA=S四边形AFGH=6,最后根据Rt△AFG的面积=3,进而得出FG的长.
解:过点A作AH⊥BC于H,如图所示:
在△ABC与△AED中,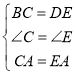 ,
,
∴△ABC≌△ADE(SAS),
∴AD=AB,S△ABC=S△AED,
又∵AF⊥DE,
即![]() ×DE×AF=
×DE×AF=![]() ×BC×AH,
×BC×AH,
∴AF=AH,
又∵AF⊥DE,AH⊥BC,
∴在Rt△AFG和Rt△AHG中,![]() ,
,
∴Rt△AFG≌Rt△AHG(HL),
同理:Rt△ADF≌Rt△ABH(HL),
∴S四边形DGBA=S四边形AFGH=6,
∵Rt△AFG≌Rt△AHG,
∴Rt△AFG的面积=3,
∵AF=![]() ,
,
∴![]() ×FG×
×FG×![]() =3,
=3,
解得:FG=4;
故答案为:4.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目




