题目内容
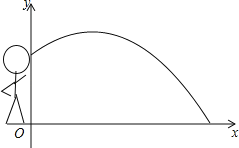
【题目】如图,一名运动员推铅球,已知铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系始终是y=ax2+![]() x+
x+![]() (a为常数,a<0).
(a为常数,a<0).
(1)解释上述函数表达式中“![]() ”的实际意义;
”的实际意义;
(2)当a=﹣![]() 时,这名运动员能把铅球推出多远?
时,这名运动员能把铅球推出多远?
(3)若这名运动员某次将铅球推出的距离不小于(2)中的距离,写出此时a的取值范围.
【答案】(1)运动员推出铅球前铅球被举起的高度;(2)这名运动员能把铅球推出10m远;(3)﹣![]() ≤a<0.
≤a<0.
【解析】
(1)上述函数表达式中“![]() ”是运动员推出铅球前铅球被举起的高度;
”是运动员推出铅球前铅球被举起的高度;
(2)当a=-![]() 时,令y=0,得到关于x的一元二次方程,解方程并根据问题的实际意义对方程的解作出取舍即可;
时,令y=0,得到关于x的一元二次方程,解方程并根据问题的实际意义对方程的解作出取舍即可;
(3)二次函数的二次项系数的绝对值越大,图象开口越小,反之亦然,据此求解即可.
(1)“![]() ”的实际意义是运动员推出铅球前铅球被举起的高度.
”的实际意义是运动员推出铅球前铅球被举起的高度.
(2)当a=﹣![]() 时,y=﹣
时,y=﹣![]() x2+
x2+![]() x+
x+![]()
当y=0时,﹣![]() x2+
x2+![]() x+
x+![]() =0
=0
解得:x1=10,x2=﹣2(不合题意,舍去)
∴这名运动员能把铅球推出10m远.
(3)若这名运动员某次将铅球推出的距离不小于(2)中的距离,
则铅球的落地点要等于或远于(2)中的落地点,从二次函数图象来看,当开口变大时即可达到要求.
∵二次函数的二次项系数a的绝对值越小,则开口越大,又已知a<0
∴﹣![]() ≤a<0.
≤a<0.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目