题目内容
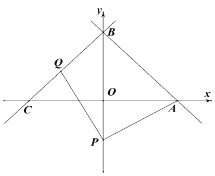
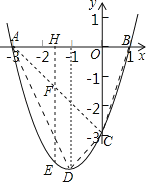
【题目】在平面直角坐标系xOy中(如图),已知经过点A(﹣3,0)的抛物线y=ax2+2ax﹣3与y轴交于点C,点B与点A关于该抛物线的对称轴对称,D为该抛物线的顶点.
(1)直接写出该抛物线的对称轴以及点B的坐标、点C的坐标、点D的坐标;
(2)联结AD、DC、CB,求四边形ABCD的面积;
(3)联结AC.如果点E在该抛物线上,过点E作x轴的垂线,垂足为H,线段EH交线段AC于点F.当EF=2FH时,求点E的坐标.
【答案】(1)对称轴为x=﹣1,点B、C、D的坐标依次为(1,0),(0,﹣3),(﹣1,﹣4);(2)9;(3)(﹣2,﹣3).
【解析】
(1)由题意可知该抛物线的对称轴为直线x=![]() =﹣1,而点A(-3,0),求出点B的坐标,进而求解;
=﹣1,而点A(-3,0),求出点B的坐标,进而求解;
(2)根据题意将四边形ABCD的面积分解为△DAM、梯形DMOC、△BOC的面积和,即可求解;
(3)根据题意设点E(x,x2+2x-3),则点F(x,-x-1),求出EF、FH长度的表达式,即可求解.
解:(1)∵该抛物线的对称轴为直线x=![]() =﹣1,而点A(﹣3,0),
=﹣1,而点A(﹣3,0),
∴点B的坐标为(1,0),
∵c=﹣3,故点C的坐标为(0,﹣3),
∵函数的对称轴为x=﹣1,故点D的坐标为(﹣1,﹣4);
(2)过点D作DM⊥AB,垂足为M,
则OM=1,DM=4,AM=2,OB=1,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ ![]() ;
;
(3)设直线AC的表达式为:y=kx+b,则![]() ,解得:
,解得:![]() ,
,
故直线AC的表达式为:y=﹣x﹣3,
将点A的坐标代入抛物线表达式得:9a﹣6a﹣3=0,解得:a=1,
故抛物线的表达式为:y=x2+2x﹣3,
设点E(x,x2+2x﹣3),则点F(x,﹣x﹣1),
则EF=(﹣x﹣1)﹣(x2+2x﹣3)=﹣x2﹣3x,FH=x+3,
∵EF=2FH,
∴﹣x2﹣3x=2(x+3),解得:x=﹣2或﹣3(舍去﹣3),
故m=﹣2.
故点E的坐标为:(﹣2,﹣3).

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有2000名居民,试估计该小区居民一周内使用共享单车的总次数.
【题目】某社区为了加强居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与作答《2020年新型冠状病毒肺炎的防护全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从该社区抽取40名居民的答卷,并对他们的成绩(单位:分)进行整理、分析,过程如下:
收集数据
85 65 95 100 90 95 85 65 75 85 100 90 70 90 100 80 80 100 95 75 80 100 80 95 65 100 90 95 85 80 100 75 60 90 70 80 95 75 100 90
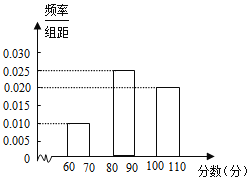
整理数据(每组数据可含最低值,不含最高值)
分组(分) | 频数 | 频率 |
60~70 | 4 | 0.1 |
70~80 | a | b |
80~90 | 10 | 0.25 |
90~100 | c | d |
100~110 | 8 | 0.2 |
分析数据
(1)填空:a= ,b= ,c= ,d= ;
(2)补全频率分布直方图;
(3)由此估计该社区居民在线答卷成绩在 (分)范围内的人数最多;
(4)如果该社区共有800人参与答卷,那么可估计该社区成绩在90分及以上约为 人.