题目内容
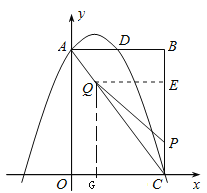
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
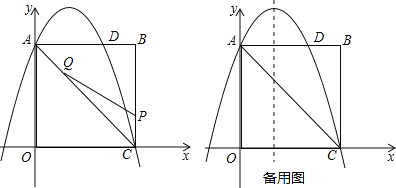
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+8;(2)①S=﹣
x+8;(2)①S=﹣![]() m2+3m;②满足条件的点F共有四个,坐标分别为F1(
m2+3m;②满足条件的点F共有四个,坐标分别为F1(![]() ,8),F2(
,8),F2(![]() ,4),F3(
,4),F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ).
).
【解析】
(1)将A、C两点坐标代入抛物线y=![]() x2+bx+c,即可求得抛物线的解析式;
x2+bx+c,即可求得抛物线的解析式;
(2)①先用m表示出QE的长度,进而求出三角形的面积S关于m的函数;
②先求出m=5时S取最大值,再根据△DFQ为直角三角形分情况求出F的坐标.
(1)将A、C两点坐标代入抛物线,得
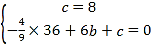 ,
,
解得:![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+8;
x+8;
(2)①∵OA=8,OC=6,
∴AC=![]() =10,
=10,
过点Q作QE⊥BC与E点,则sin∠ACB=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴QE=![]() (10﹣m),
(10﹣m),
∴S=![]() CPQE=
CPQE=![]() m×
m×![]() (10﹣m)=﹣
(10﹣m)=﹣![]() m2+3m;
m2+3m;
②∵S=﹣![]() m2+3m=﹣
m2+3m=﹣![]() (m﹣5)2+
(m﹣5)2+![]() ,
,
∴当m=5时,S取最大值;
在抛物线对称轴l上存在点F,使△FDQ为直角三角形,
∵抛物线的解析式为y=﹣![]() x2+
x2+![]() x+8的对称轴为x=
x+8的对称轴为x=![]() ,
,
∴D的坐标为(3,8),
∵CP=AQ=5,
∴CQ=5
过Q点作QG⊥x轴,
∴sin∠ACO=![]() =
=![]()
即![]()
∴QG=4
∴CG=![]()
∴OG=CO-CG=3
∴Q(3,4),
设F(![]() ,n),
,n),
当∠FDQ=90°时,则F在直线AB上,
∴F1(![]() ,8),
,8),
当∠FQD=90°时,则F的纵坐标与Q点纵坐标相同,
∴F2(![]() ,4),
,4),
当∠DFQ=90°时,设F(![]() ,n),
,n),
则FD2+FQ2=DQ2,
即![]() +(8﹣n)2+
+(8﹣n)2+![]() +(n﹣4)2=16,
+(n﹣4)2=16,
解得:n=6±![]() ,
,
∴F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ),
),
满足条件的点F共有四个,坐标分别为F1(![]() ,8),F2(
,8),F2(![]() ,4),F3(
,4),F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ).
).

 名校课堂系列答案
名校课堂系列答案