题目内容
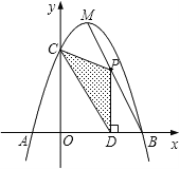
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,且点
,且点![]() 与点
与点![]() 的坐标分别为
的坐标分别为![]() .
.![]() ,点
,点![]() 是抛物线的顶点.点
是抛物线的顶点.点![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,若
,若![]() .
.
(1)求二次函数解析式;
(2)设![]() 的面积为
的面积为![]() ,试判断
,试判断![]() 有最大值或最小值?若有,求出其最值,若没有,请说明理由;
有最大值或最小值?若有,求出其最值,若没有,请说明理由;
(3)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?若存在,请写出点
为直角三角形?若存在,请写出点![]() 的坐标若不存在,请说明理由.
的坐标若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.
【解析】
(1)将点B,C的坐标代入y=-x2+bx+c即可;
(2)把(1)中的一般式配成顶点式可得到M(1,4),设直线BM的解析式为y=kx+n,再利用待定系数法求出直线BM的解析式,则P(m,-2m+6)(1≤m<3),于是根据三角形面积公式得到S=-m2+3m,然后根据二次函数的性质即可解决问题;
(3)讨论:∠PDC不可能为90°;当∠DPC=90°时,易得-2m+6=3,解方程求出m即可得到此时P点坐标;当∠PCD=90°时,利用勾股定理得到和两点间的距离公式得到m2+(-2m+3)2+32+m2=(-2m+6)2,然后解方程求出满足条件的m的值即可得到此时P点坐标.
解:(1)把![]() ,
,![]() 代入
代入![]() ,
,
得![]()
解得![]()
∴抛物线解析式为:![]() ;
;
(2)∵![]() ,
,
∴顶点![]() ,
,
∵![]() ,
,
∴设![]() 的解析式为:
的解析式为:![]()
![]()
则有![]()
解得![]() ,
,
∴![]() 的解析式为:
的解析式为:![]() ,
,
∵![]() ,
,![]() 轴
轴
∴![]() ,则
,则![]() ,
,![]() ,
,
∴![]()
![]()
![]() ,
,
∵![]()
∴![]() 有最大值,
有最大值,
当![]() 时,
时,![]() ;
;
(3)存在,
①![]() 时,如图①
时,如图①
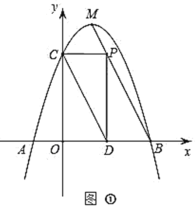
∵![]() 轴
轴
∴![]() 时,
时,![]() 轴
轴
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴此时![]() ;
;
②![]() 时,如图②,
时,如图②,
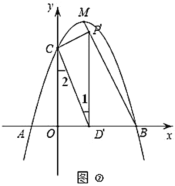
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]()
![]() ,
,
∴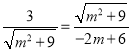 ,
,
∴![]() ,
,
![]() ,
,
解得:![]() (舍),
(舍),![]() ,
,
∴![]() ;
;
③∵![]() 轴,
轴,![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,
∴![]() 不可能等于
不可能等于![]() ;
;
综上所述,![]() 或
或![]() .
.

【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有2000名居民,试估计该小区居民一周内使用共享单车的总次数.