Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°ŅŌ¬√ś «–°∑Ĺ…Ťľ∆Ķń°į◊ų“ĽłŲ30°„Ĺ«°ĪĶń≥ŖĻś◊ųÕľĻż≥Ő£ģ
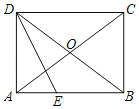
“—÷™£ļ÷ĪŌŖABľį÷ĪŌŖABÕ‚“ĽĶ„P£ģ
«ů◊ų£ļ÷ĪŌŖAB…Ō“ĽĶ„C£¨ ĻĶ√°ŌPCB£Ĺ30°„£ģ
◊ų∑®£ļ
ĘŔ‘ŕ÷ĪŌŖAB…Ō»°“ĽĶ„M£Ľ
Ęŕ“‘Ķ„Pő™‘≤–ń£¨PMő™įŽĺ∂Ľ≠Ľ°£¨”Ž÷ĪŌŖABĹĽ”ŕĶ„M°ĘN£Ľ
ĘŘ∑÷Īū“‘M°ĘNő™‘≤–ń£¨PMő™įŽĺ∂Ľ≠Ľ°£¨‘ŕ÷ĪŌŖABŌ¬∑ĹŃĹĽ°ĹĽ”ŕĶ„Q£ģ
ʋѨŔPQ£¨ĹĽAB”ŕĶ„O£ģ
Ę›“‘Ķ„Pő™‘≤–ń£¨PQő™įŽĺ∂Ľ≠Ľ°£¨ĹĽ÷ĪŌŖAB”ŕĶ„C«“Ķ„C‘ŕĶ„OĶń◊ů≤ŗ£ģ‘Ú°ŌPCBĺÕ «ňý«ů◊ųĶńĹ«£ģ
łýĺ›–°∑Ĺ…Ťľ∆Ķń≥ŖĻś◊ųÕľĻż≥Ő£¨
£®1£© Ļ”√÷Ī≥ŖļÕ‘≤Ļś≤Ļ»ęÕľ–ő£Ľ£®Ī£ŃŰ◊ųÕľļŘľ££©
£®2£©ÕÍ≥…Ō¬√śĶń÷§√ų£ģ
÷§√ų£ļ°ŖPM£ĹPN£ĹQM£ĹQN£¨
°ŗňńĪŖ–őPMQN «°° °°£ģ
°ŗPQ°ÕMN£¨PQ£Ĺ2PO£®°° °°£©£ģ£®ŐÓ–īÕ∆ņŪ“ņĺ›£©
°Ŗ‘ŕRt°ųPOC÷–£¨sin°ŌPCB£Ĺ![]() £Ĺ°° °°£®ŐÓ–ī ż÷Ķ£©
£Ĺ°° °°£®ŐÓ–ī ż÷Ķ£©
°ŗ°ŌPCB£Ĺ30°„£ģ

°ĺīūįł°Ņ£®1£©ľŻĹ‚őŲ£Ľ£®2£©Ń‚–ő£¨Ń‚–ő∂‘Ĺ«ŌŖĽ•ŌŗīĻ÷Ī∆Ĺ∑÷£¨![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›Õľ÷–ňýłÝĶń◊ųÕľ≤Ĺ÷Ť£¨≤Ļ»ęÕľ–ő£¨Ī£ŃŰ◊ųÕľļŘľ££ģ
£®2£©łýĺ›Ń‚–őĶńŇ–∂®”Ž–‘÷ £¨ľīŅ…Õ∆Ķ√ňńĪŖ–őPMQN «Ń‚–ő£ģŃ‚–ő∂‘Ĺ«ŌŖĽ•ŌŗīĻ÷Ī∆Ĺ∑÷£¨Ņ…Ķ√PQ°ÕMN£¨PQ£Ĺ2PO£¨ņŻ”√’żŌ“ļĮ żľīŅ…«ůĶ√ňý◊ųĶńĹ– «30°„Ĺ«£ģ
£®1£©»ÁÕľľīő™≤Ļ»ęĶńÕľ–ő£Ľ
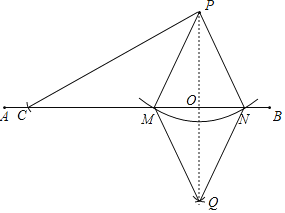
£®2£©ÕÍ≥…Ō¬√śĶń÷§√ų£ģ
°ŖPM£ĹPN£ĹQM£ĹQN£¨
°ŗňńĪŖ–őPMQN «Ń‚–ő£ģ
°ŗPQ°ÕMN£¨PQ£Ĺ2PO£®Ń‚–ő∂‘Ĺ«ŌŖĽ•ŌŗīĻ÷Ī∆Ĺ∑÷£©£ģ
°Ŗ‘ŕRt°ųPOC÷–£¨sin°ŌPCB£Ĺ![]() £¨
£¨
°ŗ°ŌPCB£Ĺ30°„£ģ
Ļ īūįłő™£ļŃ‚–ő£¨Ń‚–ő∂‘Ĺ«ŌŖĽ•ŌŗīĻ÷Ī∆Ĺ∑÷£¨![]() £ģ
£ģ

 Ľ™∂ę ¶īůįś“ĽŅő“ĽŃ∑ŌĶŃ–īūįł
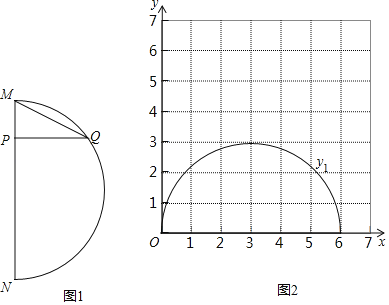
Ľ™∂ę ¶īůįś“ĽŅő“ĽŃ∑ŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘༰MNļÕŌ“MNňý◊ť≥…ĶńÕľ–ő÷–£¨P «Ō“MN…Ō“Ľ∂ĮĶ„£¨ĻżĶ„P◊ųŌ“MNĶńīĻŌŖ£¨ĹĽĽ°MN”ŕĶ„Q£¨Ń¨Ĺ”MQ£ģ“—÷™MN£Ĺ6cm£¨…ŤM°ĘPŃĹĶ„ľšĶńĺŗņŽő™xcm£¨P°ĘQŃĹĶ„ľšĶńĺŗņŽő™y1cm£¨M°ĘQŃĹĶ„ľšĶńĺŗņŽő™y2cm£ģ–°–ýłýĺ›—ßŌįļĮ żĶńĺ≠—ť£¨∑÷Īū∂‘ļĮ ży1£¨y2ňś◊‘ĪšŃŅxĶńĪšĽĮ∂ÝĪšĽĮĶńĻś¬…ĹÝ––ŃňŐĹĺŅ£ģŌ¬√ś «–°–ýĶńŐĹĺŅĻż≥Ő£¨«Ž≤Ļ≥šÕÍ’Ż£ļ
£®1£©įī’’Ō¬ĪŪ÷–◊‘ĪšŃŅxĶń÷ĶĹÝ––»°Ķ„°ĘĽ≠Õľ°Ę≤‚ŃŅ£¨∑÷ĪūĶ√ĶĹŃňy1£¨y2”ŽxĶńľł◊ť∂‘”¶÷Ķ£ļx/cm£ģ
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.24 | 2.83 | 3.00 | 2.83 | 2.24 | 0 |
y2/cm | 0 | 2.45 | 3.46 | 4.24 | m | 5.48 | 6 |
…ŌĪŪ÷–mĶń÷Ķő™°° °°£ģ£®Ī£ŃŰŃĹőĽ–° ż£©
£®2£©‘ŕÕ¨“Ľ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶxOy£®Õľ2£©÷–£¨ļĮ ży1ĶńÕľŌů»ÁÕľ£¨«Žń„√Ť≥Ų≤Ļ»ęļůĶńĪŪ÷–y2łų◊ť ż÷Ķňý∂‘”¶ĶńĶ„£®x£¨y2£©£¨≤ĘĽ≠≥ŲļĮ ży2ĶńÕľŌů£Ľ
£®3£©ĹŠļŌļĮ żÕľŌů£¨Ĺ‚ĺŲő Ő‚£ļĶĪ°ųMPQ”–“ĽłŲĹ« «30°„ Ī£¨MPĶń≥§∂»‘ľő™°° °°cm£ģ£®Ī£ŃŰŃĹőĽ–° ż£©