题目内容
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,若射线
,若射线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,就称点
为腰的等腰三角形,就称点![]() 为线段
为线段![]() 关于射线
关于射线![]() 的等腰点.
的等腰点.
(1)如图, ![]() ,
,
①若![]() ,则线段
,则线段![]() 关于射线
关于射线![]() 的等腰点的坐标是_____;
的等腰点的坐标是_____;
②若![]() ,且线段
,且线段![]() 关于射线
关于射线![]() 的等腰点的纵坐标小于1,求
的等腰点的纵坐标小于1,求![]() 的取值范围;
的取值范围;
(2) 若![]() ,且射线
,且射线![]() 上只存在一个线段
上只存在一个线段![]() 关于射线
关于射线![]() 的等腰点,则
的等腰点,则![]() 的取值范围是__________.
的取值范围是__________.
【答案】(1)(0,2);(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)①根据线段AB关于射线OC的等腰点的定义可知OP=AB=2,即可解答;
②如图,设以点![]() 为圆心,
为圆心, ![]() 为半径的圆与直线
为半径的圆与直线![]() 在第二象限的交点为
在第二象限的交点为![]() ,作
,作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,C位于D点左侧时满足条件;
,C位于D点左侧时满足条件;
(2)如图,作CH⊥y轴于H.分别以A,B为圆心,AB为半径作⊙A,⊙B,先求出∠COH=30°,由射线OC上只存在一个线段AB关于射线OC的等腰点,推出射线OC与⊙A,⊙B只有一个交点,然后讨论几种特殊情况即可找到范围.
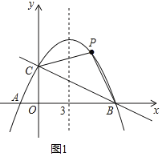
解:(1)①如图1中,由题意可知A(0,0),B(2,0),C(0,1),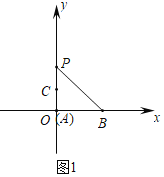
∵点P是线段AB关于射线OC的等腰点,
∴OP=AB=2,
∴P(0,2);
②如图,设以点![]() 为圆心,
为圆心, ![]() 为半径的圆与直线
为半径的圆与直线![]() 在第二象限的交点为
在第二象限的交点为![]() ,作
,作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,
,
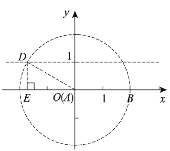
![]() ,
,
在![]() 中,根据勾股定理得
中,根据勾股定理得![]() ,
,
![]() 的取值范围是
的取值范围是![]() ;
;
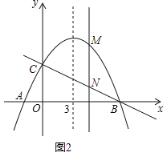
(2)如下图,作CH⊥y轴于H.分别以A,B为圆心,AB为半径作⊙A,⊙B.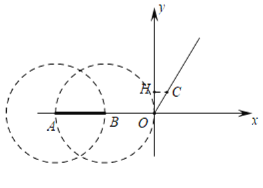
由题意C(![]() ,1),
,1),
∴CH=![]() ,OH=1,
,OH=1,
∴tan∠COH![]() ,
,
∴∠COH=30°,
当⊙B经过原点时,B(-2,0),此时t=-4,
∵射线OC上只存在一个线段AB关于射线OC的等腰点,
∴射线OC与⊙A,⊙B只有一个交点,观察图象可知当-4<t≤-2时,满足条件,
如下图,当点A在原点时,∵∠POB=60°,此时两圆的交点P在射线OC上,满足条件,此时t=0,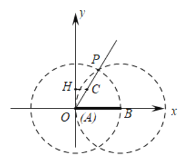
如下图,当⊙B与OC相切于P时,连接BP,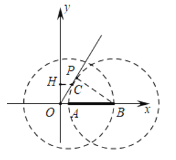
∴OC是⊙B的切线,
∴OP⊥BP,
∴∠OPB=90°,
∵BP=2,∠POB=60°,
∴![]() ,
,
∴![]() ,此时
,此时![]() ,
,
如下图,当⊙A与OC相切时,同法可得![]() ,此时
,此时![]() ,
,
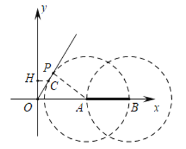
观察图形可知,满足条件的t的值为![]() ,
,
综上所述,满足条件t的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.

 灵星计算小达人系列答案
灵星计算小达人系列答案【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校![]() 名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了如下不完整的频数表和频数直方图.
名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了如下不完整的频数表和频数直方图.
被抽取的部分学生安全知识测试成绩频数表
组别 | 成绩(分) | 频数(人) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
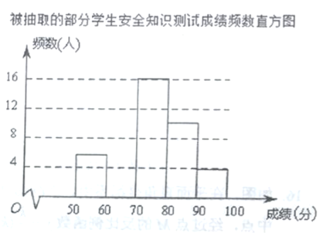
由图表中给出的信息回答下列问题:
![]() 表中的
表中的![]() ;抽取部分学生的成绩的中位数在 组;
;抽取部分学生的成绩的中位数在 组;
![]() 把上面的频数直方图补充完整;
把上面的频数直方图补充完整;
![]() 如果成绩达到
如果成绩达到![]() 分以上(包括
分以上(包括![]() 分)为优秀,请估计该校
分)为优秀,请估计该校![]() 名学生中成绩优秀的人数.
名学生中成绩优秀的人数.
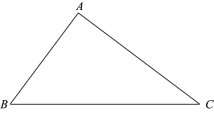
【题目】如图,在![]() 中,
中, ![]() .在同一平面内,
.在同一平面内,![]() 内部一点
内部一点![]() 到
到![]() 的距离都等于
的距离都等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() .
.
(1)直接写出![]() 的值;
的值;
(2)连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
①求证:![]() ;
;
②求直线![]() 与图形
与图形![]() 的公共点个数.
的公共点个数.
【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:
范围 |
|
|
|
|
|
|
|
人数 |
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)分析数据:样本数据的平均数、中位数、满分率如下表所示:
平均数 | 中位数 | 满分率 |
46.8 | 47.5 |
|
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数 | 中位数 | 满分率 |
45.3 | 49 |
|
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估.