题目内容
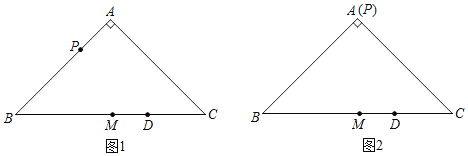
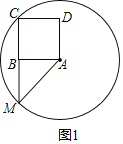
【题目】在△ABM中,∠ABM=90°,以AB为一边向△ABM的异侧作正方形ABCD,以A为圆心,AM为半径作⊙A,我们称正方形ABCD为⊙A的“关于△ABM的友好正方形”,如果正方形ABCD恰好落在⊙A的内部(或圆上),我们称正方形ABCD为⊙A的“关于△ABM的绝对友好正方形”,例如,图1中正方形ABCD是⊙A的“关于△ABM的友好正方形”.
(1)图2中,△ABM中,BA=BM,∠ABM=90°,在图中画出⊙A的“关于△ABM的友好正方形ABCD”.
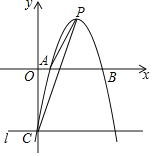
(2)若点A在反比例函数y=![]() (k>0,x>0)上,它的横坐标是2,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求k的取值范围.
(k>0,x>0)上,它的横坐标是2,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求k的取值范围.
(3)若点A是直线y=﹣x+2上的一个动点,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求出点A的横坐标m的取值范围.
【答案】(1)见解析;(2)k≥4;(3)0<m≤1或m<0.
【解析】
(1)BA=BM,∠ABM=90°,则圆的半径AM=![]() AB=AC,故点C在圆上,即可求解;
AB=AC,故点C在圆上,即可求解;
(2)分a=2、a>2、a<2三种情况,分别探究即可求解;
(3)分m=1、0<m<1、m=0、m<0、m>1五种情况,通过画图探究即可求解.
(1)∵BA=BM,∠ABM=90°,
∴圆的半径AM=![]() AB=AC,故点C在圆上,补全图形如图1,
AB=AC,故点C在圆上,补全图形如图1,
(2)设A(2,a),
当a=2时,正方形ABCD 的顶点C恰好落在⊙A上(如图2);
当a>2时,正方形ABCD 的顶点均落在⊙A内部(如图3);
当a<2时,正方形ABCD 的顶点C落在⊙A外部(如图4);
∵反比例函数![]() 过点
过点![]() ,
,
∴当a≥2时,则k≥4,
∴k的取值范围为:k≥4;
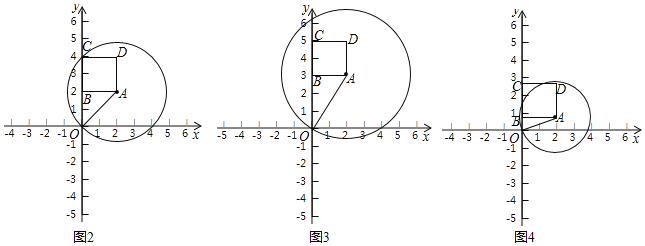
(3)当m=1时,正方形ABCD 的顶点C恰好落在⊙A上(如图5);
当0<m<1时,正方形ABCD 均落在⊙A内部(如图6);
当m=0时,△ABO 不存在;
当m<0时,正方形ABCD 均落在⊙A内部(如图7);
当m>1时,正方形ABCD 的顶点C落在⊙A外部(如图8),(当m=2时△ABO不存在);
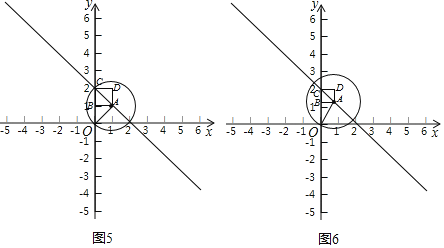
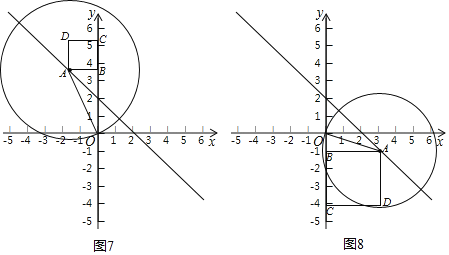
综上分析,点A的横坐标m的取值范围为:0<m≤1或m<0.

 阅读快车系列答案
阅读快车系列答案【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?