题目内容
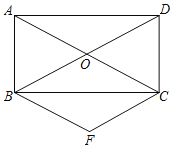
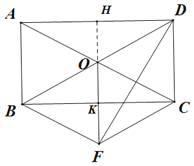
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,过B点作BF∥AC,过C点作CF∥BD,BF与CF相交于点F.
(1)求证:四边形BFCO是菱形;
(2)连接OF、DF,若AB=2,tan∠OFD=![]() ,求AC的长.
,求AC的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)先证明四边形OBFC是平行四边形,然后根据矩形的性质可知OB=OC,从而得证.
(2)连接FO并延长交AD于H,交BC于K,根据矩形、菱形的判定与性质可求出AB与BC的长度,根据勾股定理可求出AC的值.
解:(1)∵BF∥AC,CF∥BD,
∴四边形OBFC是平行四边形,
∵矩形ABCD,
∴![]()
∴OB=OC,
∴四边形OBFC是菱形.
(2)如图,连接FO并延长交AD于H,交BC于K,
∵菱形OBFC,
∴∠BKO=90°,
∵矩形ABCD,
∴∠DAB=∠ABC=90°,OA=OD,
∴四边形ABKH是矩形,
∴∠DHF=90°,HK=AB=2,
∴H是AD中点,
∵O是BD中点,
∴OH=![]() ,
,
∴FK=OK=OH=1,
∴HF=3,
∵tan∠OFD=![]() ,
,
∴HD=AH=2,
∴BC=AD=4,
由勾股定理得:![]() .
.

练习册系列答案
相关题目
【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校![]() 名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了如下不完整的频数表和频数直方图.
名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了如下不完整的频数表和频数直方图.
被抽取的部分学生安全知识测试成绩频数表
组别 | 成绩(分) | 频数(人) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
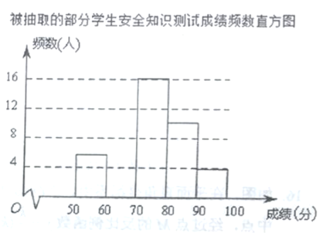
由图表中给出的信息回答下列问题:
![]() 表中的
表中的![]() ;抽取部分学生的成绩的中位数在 组;
;抽取部分学生的成绩的中位数在 组;
![]() 把上面的频数直方图补充完整;
把上面的频数直方图补充完整;
![]() 如果成绩达到
如果成绩达到![]() 分以上(包括
分以上(包括![]() 分)为优秀,请估计该校
分)为优秀,请估计该校![]() 名学生中成绩优秀的人数.
名学生中成绩优秀的人数.