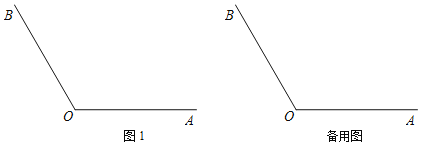��Ŀ����
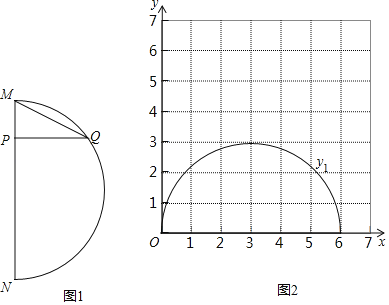
����Ŀ����ͼ1���ڻ�MN����MN����ɵ�ͼ���У�P����MN��һ���㣬����P����MN�Ĵ��ߣ�����MN�ڵ�Q������MQ����֪MN��6cm����M��P�����ľ���Ϊxcm��P��Q�����ľ���Ϊy1cm��M��Q�����ľ���Ϊy2cm��С������ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����������С����̽�����̣��벹��������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ��x/cm��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.24 | 2.83 | 3.00 | 2.83 | 2.24 | 0 |
y2/cm | 0 | 2.45 | 3.46 | 4.24 | m | 5.48 | 6 |
�ϱ���m��ֵΪ�� ������������λС����
��2����ͬһƽ��ֱ������ϵxOy��ͼ2���У�����y1��ͼ����ͼ�����������ȫ��ı���y2������ֵ����Ӧ�ĵ㣨x��y2��������������y2��ͼ��
��3����Ϻ���ͼ������⣺����MPQ��һ������30��ʱ��MP�ij���ԼΪ�� ��cm����������λС����
���𰸡���1��4.90����2������������3��1.50��4.50��
��������
��1����������ֱ�����ò��������з������������⼴�ɣ�
��2��������ֱ��������㻭������ͼ�ɣ�
��3������������ͼ���������y1��ֱ��y=![]() x��ֱ��y=
x��ֱ��y=![]() x�Ľ���ĺ����꼴�ɽ�����⣮
x�Ľ���ĺ����꼴�ɽ�����⣮
�⣺��1�����ò�������֪����x��4ʱ��y2��4.90��
��m��4.90��
�ʴ�Ϊ��4.90��
��2������ͼ����ͼ��ʾ��
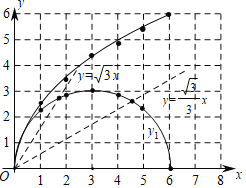
��3������y1��ֱ��y��![]() x�Ľ���ĺ�����Ϊ1.50��
x�Ľ���ĺ�����Ϊ1.50��
����y1��ֱ��y��![]() x�Ľ���ĺ�����Ϊ4.50��
x�Ľ���ĺ�����Ϊ4.50��
�ʵ���MPQ��һ������60��ʱ��MP�ij���ԼΪ1.50��4.50��
�ʴ�Ϊ��1.50��4.50��

����Ŀ��ij����Ӧ�����������������ĺ��٣�������������Ϊ�����������ɻ�����к������������������࣬���ֱ���������Ӧ�������䣮Ϊ�˽��������������������������Ը����������������ܼ�1000�������������зּ��ͳ�����������
���������� ������ �������ࣨ�֣� | �������������� | ���ɻ��������� | ���к��������� | �������������� |
�������� | 400 | 100 | 40 | 60 |
�ɻ����� | 30 | 140 | 10 | 20 |
����� | 5 | 20 | 60 | 15 |
�������� | 25 | 15 | 20 | 40 |

��������˵����
��1����������Ͷ�Ŵ������400t��
��2�����ƿɻ�����Ͷ����ȷ�ĸ���ԼΪ![]() ��
��
��3��������ʾ�����������ж����ڸ���������ŵ��������Ӧ�ü����Ծ������������������Ŀ��գ�������ȷ�ĸ����ǣ�������
A.0B.1C.2D.3
����Ŀ��������ʦΪ�˽ⱾУ���꼶Ů��1���ӡ���������������������Ŀ�Ĵ��������Ӹ�У���꼶136��Ů���У������ȡ��20��Ů����������1���������������ԣ�����������£�
�ռ����ݣ���ȡ20��Ů����1���������������Գɼ�(��)���£�
��38��46��42��52��55��43��59��46��25��38
��35��45��51��48��57��49��47��53��58��49
��1���������������ݣ����㰴���·��������������������ݣ������б���������
��Χ |
|
|
|
|
|
|
|
���� |
(˵����ÿ�����������������ﵽ49��������ʱ���п����������п��Եõ�����)
��2���������ݣ��������ݵ�ƽ��������λ�������������±���ʾ��
ƽ���� | ��λ�� | ������ |
46.8 | 47.5 |
|
�ó����ۣ��ٹ��Ƹ�У���꼶Ů�����п�����������1���ӡ�������������Ŀ���Եõ����ֵ�������
�ڸ������������صľ��꼶Ů����1���ӡ�����������������Գɼ����£�
ƽ���� | ��λ�� | ������ |
45.3 | 49 |
|
�����ϸ�У�������Գɼ�������������Գɼ���Ϊ��У���꼶Ů����1���ӡ�������������������һ��������