��Ŀ����
����Ŀ����֪һ�κ���y=��![]() x+
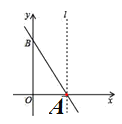
x+![]() ��ͼ����x�ᡢy��ֱ���A��B���㣮ֱ��l����A�Ҵ�ֱ��x�ᣮ������D��E�ֱ��A B�����ʱ������O���˶����˶���O��ֹͣ�����˶��ٶȷֱ���ÿ��1����λ���Ⱥ�
��ͼ����x�ᡢy��ֱ���A��B���㣮ֱ��l����A�Ҵ�ֱ��x�ᣮ������D��E�ֱ��A B�����ʱ������O���˶����˶���O��ֹͣ�����˶��ٶȷֱ���ÿ��1����λ���Ⱥ�![]() ����λ���ȣ���G��E����ֱ��l�Գƣ�GE��AB�ڵ�F����D��E���˶�ʱ��Ϊt��s����
����λ���ȣ���G��E����ֱ��l�Գƣ�GE��AB�ڵ�F����D��E���˶�ʱ��Ϊt��s����
��1����tΪ��ֵʱ���ı��������Σ��жϴ�ʱ��AFG��AGB�Ƿ����ƣ���˵�����ɣ�
��2������ADF��ֱ��������ʱ�����BEF���BFG�����֮�ȣ�
���𰸡�(1)������;(2)![]() .
.
��������
��1���������A��B�����꣬������ɵ�EF=t��BF=2t��AF=2��2t��AD=t���Ӷ��ı���ADEFΪƽ���ı��Σ���AD=AFʱ��![]() ADEF�����ο����t��ֵ������������Ǻ�����֪ʶ������EBG=60�㣬�Ӷ���ABG=30�㣬����������ȵ��������������ƿ�֤��AFG�ס�AGB��
ADEF�����ο����t��ֵ������������Ǻ�����֪ʶ������EBG=60�㣬�Ӷ���ABG=30�㣬����������ȵ��������������ƿ�֤��AFG�ס�AGB��
��2���֡�ADF=90��͡�AFD=90�����������⼴��.
�⣺��1����������ɵã�A��1��0����B��0��![]() ������OBA=30�㣬
������OBA=30�㣬
��BE=![]() t��
t��
��EF=t��BF=2t��AF=2��2t��
��AD=t��
��EF=AD����EF��AD��
���ı���ADEFΪƽ���ı��Σ�
��AD=AFʱ��ADEF�����Σ�����t=2��2t�����t=![]() ��
��
�ڴ�ʱ��AFG���AGB���ƣ��������£�
���ͼ1��ʾ������AE����AE=AG��
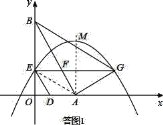
���AGE=��AEG=30�㣮
��Rt��BEG��BE=![]() ��EG=2��
��EG=2��
��tan��EBG=![]() =
=![]() ��
��
���EBG=60�㣬
���ABG=��EBG����EBF=30�㣮
�ڡ�AFG���AGB�У��ߡ�BAG=��GAF����ABG=��AGF=30�㣬
���AFG�ס�AGB��
��2���ߡ�DAF=60�㣬
�൱��ADF=90��ʱ��AF=2AD������2��2t=2t�����t=![]() ��
��
��ʱEF=![]() ��FG=
��FG=![]() ��
��
��![]() =
=![]() =
=![]() ��
��
�൱��AFD=90��ʱ��AD=2AF������t=2��2��2t�������t=![]() ��
��
��ʱEF=![]() ��FG=
��FG=![]() ��
��
��![]() =
=![]() =
=![]() ��
��

 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�