题目内容
【题目】甲、乙两人同时从圆形跑道（圆形跑道的总长小于700m）上一直径两端A，B相向起跑．第一次相遇时离A点100m，第二次相遇时离B点60m，则圆形跑道的总长为（ ）
A.240mB.360mC.480mD.600m
【答案】C
【解析】
如图所示，分两种情况考虑：第一次相遇在C点，则第二次相遇可在B点下方D点处或其上方
点处，根据两种情况分别列出方程求解即可.
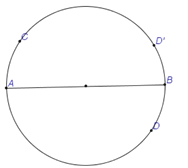
如图所示，设圆形跑道总长为2S，又设甲乙速度分别为x和y，
（1）当甲乙第一次相遇在C点，第二次相遇在B点下方D点处时，
则：
……①
……②
结合①与②得：
，解得
（舍去），
，
∴
，
经检验是原方程的解，
∴跑道长为480m；
（2）当甲乙第一次相遇在C点，第二次相遇在B点上方点处时，
则：……③
……④
结合③与④得：
，解得（舍去），
，
∴
，
经检验是原方程的解，
∵圆形跑道的总长小于700m，
∴舍去.
故选C.
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】天津市奥林匹克中心体育场—“水滴”位于天津市西南部的奥林匹克中心内，某校九年级学生由距“水滴”10千米的学校出发前往参观，一部分同学骑自行车先走，过了20分钟后，其余同学乘汽车出发，结果他们同时到达．已知汽车的速度是骑车同学速度的2倍，求骑车同学的速度．
（1）设骑车同学的速度为x千米/时，利用速度、时间、路程之间的关系填写下表．（要求：填上适当的代数式，完成表格）
速度（千米/时） | 所用时间（时） | 所走的路程（千米） | |
骑自行车 | x | 10 | |
乘汽车 | 10 |
（2）列出方程（组），并求出问题的解．
