题目内容
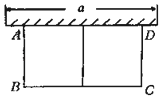
【题目】如图,有长为30米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可使用长度a=10米).设花圃的一边AB长为x米,面积为y平方米.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)如果所围成的花圃的面积为63平方米,试求宽AB的长;
(3)按题目的设计要求, (填“能”或“不能”)围成面积为80平方米的花圃.
【答案】(1)y=﹣3x2+30x;(2)AB的长为7米;(3)不能.
【解析】
(1)设AB长为x米,则BC长为:(30﹣3x)米,该花圃的面积为:(30﹣3x)x;进而得出函数关系即可;
(2)将y=63代入(1)中所求的函数关系式,得出关于x的一元二次方程,解方程求出符合题意的x的值,即是所求AB的长;
(3)将y=80代入(1)中所求的函数关系式,得出关于x的一元二次方程,利用根的判别式进行判定即可.
(1)由题意得:
y=x(30﹣3x),即y=﹣3x2+30x;
(2)当y=63时,﹣3x2+30x=63,
解此方程得x1=7,x2=3.
当x=7时,30﹣3x=9<10,符合题意;
当x=3时,30﹣3x=21>10,不符合题意,舍去;
故所围成的花圃的面积为63平方米时,宽AB的长为7米;
(3)不能围成面积为80平方米的花圃.
理由:当y=80时,﹣3x2+30x=80,
整理得3x2﹣30x+80=0,
∵△=(﹣30)2﹣4×3×80=﹣60<0,
∴这个方程无实数根,
∴不能围成面积为80平方米的花圃.
故答案为:不能.

练习册系列答案
相关题目