题目内容
【题目】如图已知数轴上点
、
分别表示
、
，且
与
互为相反数，
为原点.
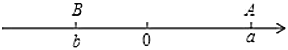
（1）
______，
______；
（2）将数轴沿某个点折叠，使得点与表示－10的点重合，则此时与点重合的点所表示的数为______；
（3）若点
、
分别从点、同时出发，点以每秒1个单位长度的速度沿数轴向左匀速运动，点以每秒2个单位长度的速度沿数轴向右匀速运动，到点后立刻原速返回，设运动时间为
秒.
①点表示的数是______（用含
的代数式表示）；
②求为何值时，
；
③求为何值时，点与相距3个单位长度.
【答案】（1）9，-6；（2）5；（3）①9-t；②t=6或t=18；③t=4、6或12
【解析】
（1）根据
与
互为相反数列式计算得出a与b；
（2）先计算得出点
与表示－10的点重合时的折叠点，再根据对称性得到答案；
（3）①根据点左右平移的规律即可解答；
②分两种情况，点M在OA之间，点M在点O左侧，根据
分别计算得出t的值即可；
③先计算出点N表示的数，再分三种情况求出t的值.
（1）∵与互为相反数，
∴+=0，
∴b+6=0，a-9=0，
∴b=-6，a=9，
故答案为：9，-6；
（2）∵点A表示的数是9，
∴当折叠，使得点与表示－10的点重合时的折叠点是
-0.5，
∴此时与点
重合的点所表示的数为-0.5+（-0.5+6）=5，
故答案为：5；
（3）①点
从点出发以每秒1个单位长度的速度沿数轴向左匀速运动，
∴点表示的数是9-t，
故答案为：9-t；
②∵，
∴当点M在OA之间时，即2（9-t）=t，解得t=6；
当点M在点O左侧时，2（t-9）=t，解得t=18；
∴当t=6或t=18时，，
③由题意知，AM=t，BN=2t，
当点N未到达点A，且与点M未相遇时，t+2t+3=15，得t=4；
当点N未到达点A，且与点M相遇后，t+2t-3=15，得t=6；
当点N到达点A后,t-（2t-15）=3，得t=12，
综上，当t=4、6或12时，点M与N相距3个单位长度.
