题目内容
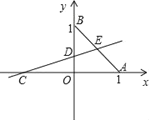
【题目】已知:如图,平面直角坐标系xOy中,B(0,1),OB=OC=OA,A、C分别在x轴的正负半轴上.过点C的直线绕点C旋转,交y轴于点D,交线段AB于点E.
(1)求∠OAB的度数及直线AB的解析式;
(2)若△OCD与△BDE的面积相等,求点D的坐标.
【答案】(1)45°,y=﹣x+1;(2)(0,![]() ).
).
【解析】
(1)根据A、B的坐标和三角形的内角和定理求出∠OAB的度数即可;设直线AB的解析式为y=kx+b,把A、B的坐标代入得出方程组,求出方程组的解即可;
(2)推出三角形AOB和三角形ACE的面积相等,根据面积公式求出E的纵坐标,代入直线AB的解析式,求出E的横坐标,设直线CE的解析式是:y=mx+n,利用待定系数法求出直线EC的解析式,进而即可求得点D的坐标.
解:(1)∵OB=OC=OA,∠AOB=90°,
∴∠OAB=45°;
∵B(0,1),
∴A(1,0),
设直线AB的解析式为y=kx+b.
∴![]()
解得,
![]()
∴直线AB的解析式为y=﹣x+1;
(2)∵S△COD=S△BDE,
∴S△COD+S四边形AODE=S△BDE+S四边形AODE,
即S△ACE=S△AOB,
∵点E在线段AB上,
∴点E在第一象限,且yE>0,
∴![]()
∴![]()
![]()
把y![]() 代入直线AB的解析式得:
代入直线AB的解析式得:![]()
∴![]()
设直线CE的解析式是:y=mx+n,
∵![]() 代入得:
代入得: 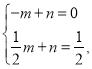
解得:![]()
∴直线CE的解析式为![]()
令x=0,则![]()
∴D的坐标为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目