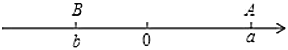题目内容
【题目】如图(1),平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.

(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点,求证:BD=OE;
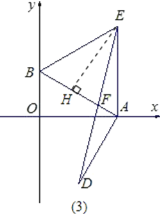
(3)在(2)的条件下,连接DE交AB于F,求证:F为DE的中点.
【答案】(1)2;(2)见解析;(3)见解析.
【解析】
(1)直接运用直角三角形30°角的性质即可.
(2)连接OD,易证△ADO为等边三角形,再证△ABD≌△AEO即可.
(3)作EH⊥AB于H,先证△ABO≌△AEH,得AO=EH,再证△AFD≌△EFH即可.
(1)解:∵在Rt△ABO中,∠BAO=30°,
∴AB=2BO=2;
(2)证明:连接OD,

∵△ABE为等边三角形,
∴AB=AE,∠EAB=60°,
∵∠BAO=30°,作OA的垂直平分线MN交AB的垂线AD于点D,
∴∠DAO=60°.
∴∠EAO=∠NAB
又∵DO=DA,
∴△ADO为等边三角形.
∴DA=AO.
在△ABD与△AEO中,
∵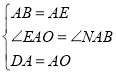 ,
,
∴△ABD≌△AEO(SAS).
∴BD=OE.
(3)证明:作EH⊥AB于H.
∵AE=BE,∴AH=![]() AB,
AB,
∵BO=![]() AB,∴AH=BO,
AB,∴AH=BO,
在Rt△AEH与Rt△BAO中,
![]() ,
,
∴Rt△AEH≌Rt△BAO(HL),
∴EH=AO=AD.
又∵∠EHF=∠DAF=90°,
在△HFE与△AFD中,
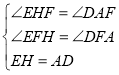 ,
,
∴△HFE≌△AFD(AAS),
∴EF=DF.
∴F为DE的中点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目