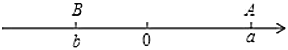ЬтФПФкШн
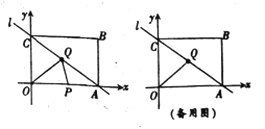
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гыxжсНЛAЁЂBСНЕуЃЈAЕудкBЕузѓВрЃЉЃЌжБЯп
гыxжсНЛAЁЂBСНЕуЃЈAЕудкBЕузѓВрЃЉЃЌжБЯп![]() гыХзЮяЯпНЛгкAЁЂCСНЕуЃЌЦфжаCЕуЕФКсзјБъЮЊ2ЃЎ
гыХзЮяЯпНЛгкAЁЂCСНЕуЃЌЦфжаCЕуЕФКсзјБъЮЊ2ЃЎ
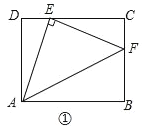
ЃЈ1ЃЉЧѓAЁЂB СНЕуЕФзјБъМАжБЯпACЕФКЏЪ§БэДяЪНЃЛ
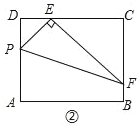
ЃЈ2ЃЉPЪЧЯпЖЮACЩЯЕФвЛИіЖЏЕуЃЌЙ§PЕузїyжсЕФЦНааЯпНЛХзЮяЯпгкEЕуЃЌЧѓЯпЖЮPEГЄЖШЕФзюДѓжЕЃЛ
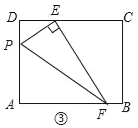
ЃЈ3ЃЉЕуGХзЮяЯпЩЯЕФЖЏЕуЃЌдкxжсЩЯЪЧЗёДцдкЕуFЃЌЪЙAЁЂCЁЂFЁЂGетбљЕФЫФИіЕуЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШчЙћДцдкЃЌЧѓГіЫљгаТњзуЬѕМўЕФFЕузјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПМћНтЮі
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉСюy=0ЃЌНтx2-2x-3=0ЃЌПЩЕУABЕФзјБъЃЛНЋCЕФКсзјБъДњШыЃЌвзЕУЦфзнзјБъЃЌНсКЯAЕФзјБъЃЌПЩЕУBCЕФЗНГЬЃЛЃЈ2ЃЉЩшГіPЕуЕФКсзјБъЃЌБэЪОГіPЁЂEЕФзјБъЃЌПЩЕУPEГЄЖШЕФБэДяЪНЃЌНјЖјИљОнxЕФШЁжЕЗЖЮЇПЩЕУЯпЖЮPEГЄЖШЕФзюДѓжЕЃЎЃЛЃЈ3ЃЉДЫРрЮЪЬтвЛЖЈЪЧвЊЗжЧщПіЬжТлЕФЃЌБОЬтПЩвдЗжЮЊ4жжЧщПіЃЌзіЬтЪБОЁСПБмУтТЉЕєНт.
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉСюy=0ЃЌНтЕУ![]() Лђ
Лђ![]()
ЁрAЃЈ-1ЃЌ0ЃЉBЃЈ3ЃЌ0ЃЉЃЛ
НЋCЕуЕФКсзјБъx=2ДњШы![]() ЕУy=-3ЃЌЁрCЃЈ2ЃЌ-3ЃЉ
ЕУy=-3ЃЌЁрCЃЈ2ЃЌ-3ЃЉ
ЁржБЯпACЕФКЏЪ§НтЮіЪНЪЧy="-x-1"
ЃЈ2ЃЉЩшPЕуЕФКсзјБъЮЊxЃЈ-1ЁмxЁм2ЃЉ
дђPЁЂEЕФзјБъЗжБ№ЮЊЃКPЃЈxЃЌ-x-1ЃЉЃЌEЃЈ![]()
ЁпPЕудкEЕуЕФЩЯЗНЃЌPE=![]() ЃЈ2ЗжЃЉ
ЃЈ2ЗжЃЉ
ЁрЕБ![]() ЪБЃЌPEЕФзюДѓжЕ=
ЪБЃЌPEЕФзюДѓжЕ=![]()
ЃЈ3ЃЉДцдк4ИіетбљЕФЕуFЃЌЗжБ№ЪЧ![]()
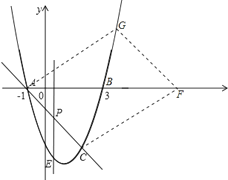
ЂйШчЭМЃЌСЌНгCгыХзЮяЯпКЭyжсЕФНЛЕуЃЌФЧУДCGЁЮxжсЃЌДЫЪБAF=CG=2ЃЌвђДЫFЕуЕФзјБъЪЧЃЈ-3ЃЌ0ЃЉЃЛ

ЂкШчЭМЃЌAF=CG=2ЃЌAЕуЕФзјБъЮЊЃЈ-1ЃЌ0ЃЉЃЌвђДЫFЕуЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЛ
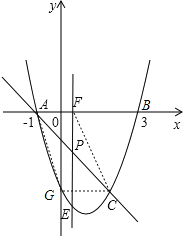
ЂлШчЭМЃЌДЫЪБCЃЌGСНЕуЕФзнзјБъЙигкxжсЖдГЦЃЌвђДЫGЕуЕФзнзјБъЮЊ3ЃЌДњШыХзЮяЯпжаМДПЩЕУГіGЕуЕФзјБъЮЊЃЈ1+![]() ЃЌ3ЃЉЃЌгЩгкжБЯпGFЕФаБТЪгыжБЯпACЕФЯрЭЌЃЌвђДЫПЩЩшжБЯпGFЕФНтЮіЪНЮЊy=-x+hЃЌНЋGЕуДњШыКѓПЩЕУГіжБЯпЕФНтЮіЪНЮЊy=-x+4+
ЃЌ3ЃЉЃЌгЩгкжБЯпGFЕФаБТЪгыжБЯпACЕФЯрЭЌЃЌвђДЫПЩЩшжБЯпGFЕФНтЮіЪНЮЊy=-x+hЃЌНЋGЕуДњШыКѓПЩЕУГіжБЯпЕФНтЮіЪНЮЊy=-x+4+![]() ЃЎвђДЫжБЯпGFгыxжсЕФНЛЕуFЕФзјБъЮЊЃЈ4+
ЃЎвђДЫжБЯпGFгыxжсЕФНЛЕуFЕФзјБъЮЊЃЈ4+![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЂмШчЭМЃЌЭЌЂлПЩЧѓГіFЕФзјБъЮЊЃЈ4-![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
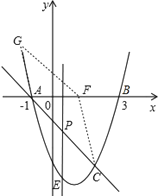
злКЯЫФжжЧщПіПЩЕУГіЃЌДцдк4ИіЗћКЯЬѕМўЕФFЕуЃЎ

 ДКгъНЬг§ЭЌВНзїЮФЯЕСаД№АИ
ДКгъНЬг§ЭЌВНзїЮФЯЕСаД№АИ