题目内容
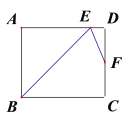
【题目】如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,当点F是CD的中点时,若AB=4,则BC=_________.
【答案】![]()
【解析】
如下图,延长EF与BC的延长线相交于点H,由已知条件易证:AE=AB=4,BE=![]() ,△DEF≌△CHF,从而可得DE=CH,∠DEF=∠H=∠BEH,从而可得BH=BE=
,△DEF≌△CHF,从而可得DE=CH,∠DEF=∠H=∠BEH,从而可得BH=BE=![]() ,设BC=
,设BC=![]() ,则AD=
,则AD=![]() ,由此可得DE=AD-AE=
,由此可得DE=AD-AE=![]() ,CH=BH-BC=
,CH=BH-BC=![]() ,由此可得
,由此可得![]() ,解此方程即可求得BC的值.
,解此方程即可求得BC的值.
如下图,延长EF与BC的延长线相交于点H,设BC=![]() ,
,
∵四边形ABCD是矩形,
∴∠A=∠D=∠HCF=∠ABC=90°,CD=AB=4,AD=BC=![]() ,AD∥BC,
,AD∥BC,
∴∠AEB=∠CBE,∠DEF=∠H,
∵BE平分∠ABC,
∴∠AEB=∠CBE=∠ABE,
∴AE=AB=4,
∴BE=![]() ,DE=AD-AE=
,DE=AD-AE=![]() ,
,
∵点F是DC的中点,EF平分∠BED,
∴DF=FC,∠DEF=∠BEF=∠H,
∴△DEF≌△CHF,BH=BE=![]() ,
,
∴DE=CH=BH-BC=![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴BC=![]() .
.


练习册系列答案
相关题目