题目内容
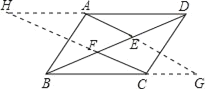
【题目】如图,在ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.

【答案】(1)△ABE≌△CDF;△AED≌△CFB;△ABD≌△CDB;(2)详见解析
【解析】
(1)因为ABCD是平行四边形,AD∥BC,因此∠ADE=∠CBF,又知DE=BF,D=BC那么构成了三角形ADE和CBF全等的条件(SAS)因此△AED≌△CFB.同理可得出△ABE≌△CDF,△ABD≌△CDB.
(2)要证明四边形AGCH是个平行四边形,已知的条件有AB∥CD,只要证得AG∥CH即可得出上述结论.那么就需要证明∠AEB=∠DFC,也就是证明△ABE≌△CDF,根据AB∥CD.∴∠ABD=∠CDB.这两个三角形中已知的条件就有AB=CD,BE=DF(BE=DF+EF=DE+EF=DF),又由上面得出的对应角相等,那么两三角形就全等了(SAS).
(1)解:△ABE≌△CDF;△AED≌△CFB;△ABD≌△CDB;
(2)证明:在△ADE和△CBF中,AD=CB,∠ADE=∠CBF,DE=BF,
∴△ADE≌△CBF,
∴∠AED=∠CFB.
∵∠FEG=∠AED=∠CFB=∠EFH,
∴AG‖HC,而且,AH‖GC,
∴四边形AGCH是平行四边形

练习册系列答案
相关题目