Question

【题目】小东根据学习一次函数的经验，对函数y=|2x﹣1|的图象和性质进行了探究．下面是小东的探究过程，请补充完成：

（1）函数y=|2x﹣1|的自变量x的取值范围是　 　；

（2）已知：

①当x=时，y=|2x﹣1|=0；

②当x＞时，y=|2x﹣1|=2x﹣1

③当x＜时，y=|2x﹣1|=1﹣2x；

显然，②和③均为某个一次函数的一部分．

（3）由（2）的分析，取5个点可画出此函数的图象，请你帮小东确定下表中第5个点的坐标（m，n），其中m=　 　；n=　 　；：

x	…	﹣2	0		1	m	…
y	…	5	1	0	1	n	…

（4）在平面直角坐标系xOy中，作出函数y=|2x﹣1|的图象；

（5）根据函数的图象，写出函数y=|2x﹣1|的一条性质．

Answer 1

【答案】见解析

【解析】

（1）函数y=|2x-1|的自变量x的取值范围是全体实数；（3）取m=3把x=3代入y=|2x-1|计算即可；（4）根据（3）中的表格描点连线即可；（5）根据函数的图象，即可求解.

解：（1）函数y=|2x-1|的自变量x的取值范围是全体实数；

故答案为：全体实数；

（3）m、n的取值不唯一，取m=3，把x=3代入y=|2x-1|，得y=|2×3-1|=5，

即m=3，y=5.

故答案为：3，5.

（4）图象如图所示；（要求描点、连线正确）

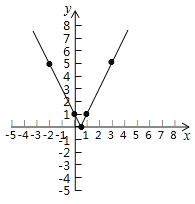
（5）答案不唯一，符合函数y的性质均可.

“点睛”此题考查了一次函数的图象与性质，掌握一次函数的性质是解题的关键.