Question

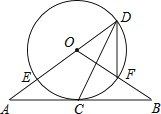
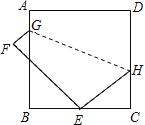
【题目】某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕着矩形ABCD（AB＜BC）的对角线交点O旋转（如图①→②→③），图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点．

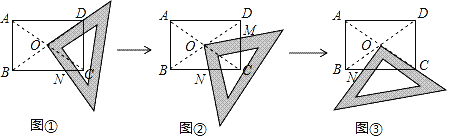
（1）该学习小组中一名成员意外地发现：在图①（三角板的一直角边与OD重合）中，BN2=CD2+CN2；在图③（三角板的一直角边与OC重合）中，CN2=BN2+CD2．请你对这名成员在图①和图③中发现的结论选择其一说明理由．

（2）试探究图②中BN、CN、CM、DM这四条线段之间的关系，写出你的结论，并说明理由．

Answer 1

【答案】(1)见解析;(2)见解析.

【解析】

（1）连接DN，根据矩形得出OB=OD，根据线段垂直平分线得出BN=DN，根据勾股定理求出DN的平方，即可求出答案；

（2）延长NO交AD于点P，连接PM，MN，证△BNO≌△DPO，推出OP=ON，DP=BN，根据线段垂直平分线求出PM=MN，根据勾股定理求出即可．

（1）选①．证明如下：连接DN，

∵四边形ABCD是矩形，∴OB=OD，

∵∠DON=90°，∴BN=DN，

∵∠BCD=90°，∴DN2=CD2+CN2，∴BN2=CD2+CN2；

（2）延长NO交AD于点P，连接PM，MN，

∵四边形ABCD是矩形，∴OD=OB，AD∥BC，∴∠DPO=∠BNO，∠PDO=∠NBO，

在△BON和△DOP中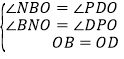，∵，∴△BON≌△DOP（AAS），∴ON=OP，BN=PD，

∵∠MON=90°，∴PM=MN，

∵∠ADC=∠BCD=90°，∴PM2=PD2+DM2，MN2=CM2+CN2，∴PD2+DM2=CM2+CN2，∴BN2+DM2=CM2+CN2．