题目内容
如图,等腰梯形ABCD内接于半圆D,且AB = 1,BC = 2,则OA =( ).


A. | B. | C. | D. |
A
分别过点B、点C作BE⊥AD于点E,CF⊥AD于点F,再过点O作OG⊥BC于点G,连接OB,
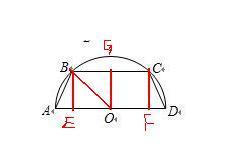
因为四边形ABCD是等腰梯形,AB=1,BC=2,
则BE=OG=CF,BG=GC=EO=OF=EF/2=BC/2=2/2=1,AB=CD=1,
设OA=OD=OB= ,
,
则AE= -1,
-1,
所以BE=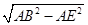 =
=  =
=  ,
,
又因为OG= =
=  ,
,
又因为OG=BE,
所以 =(
=( -1),
-1),
所以2 -
- =
= -1,
-1,
则2 -2
-2 -1=0,
-1=0,
则 =
=  或
或 (舍去),
(舍去),
即OA= 。
。

因为四边形ABCD是等腰梯形,AB=1,BC=2,
则BE=OG=CF,BG=GC=EO=OF=EF/2=BC/2=2/2=1,AB=CD=1,
设OA=OD=OB=
 ,
,则AE=
 -1,
-1,所以BE=
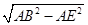 =
=  =
=  ,
,又因为OG=
 =
=  ,
,又因为OG=BE,
所以
 =(
=( -1),
-1),所以2
 -
- =
= -1,
-1,则2
 -2
-2 -1=0,
-1=0,则
 =
=  或
或 (舍去),
(舍去),即OA=
 。
。
练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 的坡度为
的坡度为
 与水平宽度
与水平宽度 的比),
的比),
 =
= .
.
 ,
, .试计算此改建需占路面的宽度
.试计算此改建需占路面的宽度 的长(结果精确0.01)
的长(结果精确0.01)



 的位置如图3所示,则
的位置如图3所示,则  的值是
的值是


