题目内容
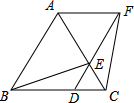
如图，梯形ABCD中，AD∥BC，点M是BC的中点，且MA＝MD．
求证：四边形ABCD是等腰梯形．
求证：四边形ABCD是等腰梯形．
略
证明：∵ MA＝MD，∴ △MAD是等腰三角形，
∴ ∠DAM＝∠ADM． ……（1分）
∵ AD∥BC，
∴ ∠AMB＝∠DAM，∠DMC＝∠ADM．
∴ ∠AMB＝∠DMC． ……（3分）
又∵ 点M是BC的中点，∴ BM＝CM． ……（4分）
在△AMB和△DMC中，
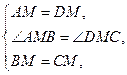
∴ △AMB≌△DMC． ……（5分）
∴ AB＝DC，四边形ABCD是等腰梯形． ……（6分）
∴ ∠DAM＝∠ADM． ……（1分）
∵ AD∥BC，
∴ ∠AMB＝∠DAM，∠DMC＝∠ADM．
∴ ∠AMB＝∠DMC． ……（3分）
又∵ 点M是BC的中点，∴ BM＝CM． ……（4分）
在△AMB和△DMC中，
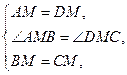
∴ △AMB≌△DMC． ……（5分）
∴ AB＝DC，四边形ABCD是等腰梯形． ……（6分）
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
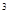，求原铁皮的长
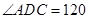°，则B、D两点之间的距离为（ ）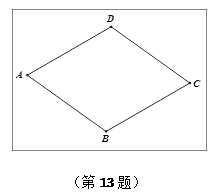
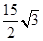C.7.5 D.15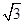
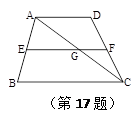
，若AD︰BC = 2︰3. 请探究：当k为下列三种情况时，四边形ABPE是什么四边形？①当
△ADE ；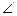
BHD的度数，并说明理由；
，△ADG的面积为
，判断
，点E是折线段A－D－C上的一个动点（点E与点A不重合），点P是点A关于BE的对称点．
