题目内容
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价x的范围.
(1) y=-x+120(60≤x≤87);(2) W=-(x-90)2+900,87,891;(3)70≤x≤87.
解析试题分析:(1)直接把点(65,55)、(75,45)代入一次函数解析式,联立方程组求解k,b的值,则函数解析式可求;
(2)由每一件的利润乘以销售量得利润函数,利用配方法求最大值;
(3)求解不等式,结合实际问题的定义域得到获得利润不低于500元时的销售单价x的范围.
试题解析:根据题意得 ,解得k=-1,b=120.
,解得k=-1,b=120.
∴所求一次函数的表达式为y=-x+120(60≤x≤87);
(2)每一件的获利为x-60,
则获得利润W=(x-60)•(-x+120)=-x2+180x-7200=-(x-90)2+900,
∵抛物线的开口向下,∴当x<90时,W随x的增大而增大,而60≤x≤87,
∴当x=87时,W=-(87-90)2+900=891,
∴当销售单价定为87元时,商场可获得最大利润,最大利润是891元;
(3)由-x2+180x-7200≥500,
整理得,x2-180x+7700≤0,解得,70≤x≤110,
∴要使该商场获得利润不低于500元,销售单价应在70元到110元之间,而60≤x≤87,
∴销售单价x的范围是70≤x≤87.
考点: 函数模型的选择与应用.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案某公司有甲种原料260kg,乙种原料270kg,计划用这两种原料生产A、B两种产品共40件.生产每件A种产品需甲种原料8kg,乙种原料5kg,可获利润900元;生产每件B种产品需甲种原料4kg,乙种原料9kg,可获利润1100元.设安排生产A种产品x件.
(1)完成下表
| | 甲(kg) | 乙(kg) | 件数(件) |
| A | | 5x | x |
| B | 4(40-x) | | 40-x |
(3)设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润.
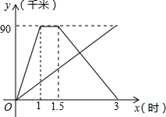
我市某工艺厂为配合奥运会,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
| 销售单价x(元/件) | …… | 30 | 40 | 50 | 60 | …… |
| 每天销售量y(件) | …… | 500 | 400 | 300 | 200 | …… |

(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
 与一次函数
与一次函数 的图象交于A(3,1)、B(m,-3)两点.
的图象交于A(3,1)、B(m,-3)两点. OA,请直接写出点P的坐标.
OA,请直接写出点P的坐标.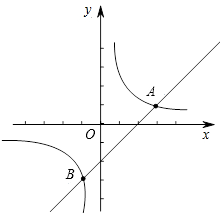
 与
与 的图象相交于A点,函数
的图象相交于A点,函数 轴、
轴、 轴于点B,C,函数
轴于点B,C,函数
 的面积
的面积 与
与 成正比例,且当
成正比例,且当 时,
时, .
. 与
与 的函数关系式;
的函数关系式; 时的函数值.
时的函数值.