题目内容
【题目】已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m、n的值
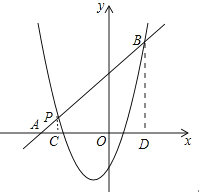
(2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
【答案】
(1)
解:∵对称轴是经过(﹣1,0)且平行于y轴的直线,
∴﹣![]() =﹣1,
=﹣1,
∴m=2,
∵二次函数y=x2+mx+n的图象经过点P(﹣3,1),
∴9﹣3m+n=1,得出n=3m﹣8.
∴n=3m﹣8=﹣2
(2)
解:∵m=2,n=﹣2,
∴二次函数为y=x2+2x﹣2,
作PC⊥x轴于C,BD⊥x轴于D,则PC∥BD,
∴![]() =
=![]() ,
,
∵P(﹣3,1),
∴PC=1,
∵PA:PB=1:5,
∴![]() =
=![]() ,
,
∴BD=6,
∴B的纵坐标为6,
代入二次函数为y=x2+2x﹣2得,6=x2+2x﹣2,
解得x1=2,x2=﹣4(舍去),
∴B(2,6),
∴![]() ,解得
,解得![]() ,
,
∴一次函数的表达式为y=x+4.
【解析】(1)利用对称轴公式求得m,把P(﹣3,1)代入二次函数y=x2+mx+n得出n=3m﹣8,进而就可求得n;
(2)根据(1)得出二次函数的解析式,根据已知条件,利用平行线分线段成比例定理求得B的纵坐标,代入二次函数的解析式中求得B的坐标,然后利用待定系数法就可求得一次函数的表达式.
【考点精析】掌握确定一次函数的表达式是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.

练习册系列答案
相关题目