Question

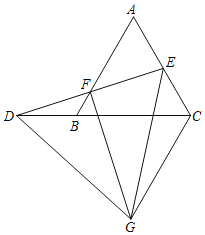
【题目】如图，在等边△ABC中，点D为CB延长线上一点，点E是AC的中点，连接DE交AB于点F，以DE为边向下作等边△DEG，连接CG、FG，若FG⊥DE，BD+BF＝7，则CG的长为_____．

Answer 1

【答案】

【解析】

取AB，BC的中点M，N．首先证明四边形EMBN是菱形，再证明DN＝CG，DB＝BN＝EN＝2BF，求出DB即可解决问题．

解：取AB，BC的中点M，N．

∵△ABC是等边三角形，

∴AB＝BC＝AC，∠ACB＝60°，

∵AM＝BM，AE＝EC，CN＝BN，

∴EM∥BC，EN∥AB，EM＝BC，EN＝AB，

∴四边形EMBN是平行四边形，

∵EM＝EN，

∴四边形EMBN是菱形，

∵△EDG，△ECN是等边三角形，

∴ED＝EG，EN＝EC，∠DEG＝∠NEC，

∴∠DEN＝∠GEC，

∴△DEN≌△GEC（SAS），

∴CG＝DN，

∵CF⊥DE，GD＝GE，

∵DF＝EF，

∵BF∥EN，

∴DB＝BN，

∴EN＝2BF，设BF＝a，则EN＝BN＝DB＝2a，

∵DB+BF＝7，

∴3a＝7，

∴a＝，

∴CG＝DN＝2BD＝，

故答案为： ．