题目内容
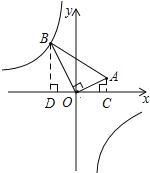
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(4,2),BO=4![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为_____.
的图象经过点B,则k的值为_____.

【答案】﹣32
【解析】
根据∠AOB=90°,过点A作AC⊥x轴,过点B作BD⊥x轴,证明△DBO∽△COA,再利用相似三角形的对应边成比例,列出比例式进行计算,求得点B的坐标,进而得出k的值.
过点A作AC⊥x轴,过点B作BD⊥x轴,垂足分别为C、D,则∠OCA=∠BDO=90°,
∴∠DBO+∠BOD=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠DBO=∠AOC,
∴△DBO∽△COA,
∴![]() ,
,
∵点A的坐标为(4,2),
∴AC=2,OC=4,
∴AO=![]() ,
,
∴![]() ,即BD=8,DO=4,
,即BD=8,DO=4,
∴B(-4,8),
∵反比例函数y=![]() 的图象经过点B,
的图象经过点B,
∴k的值为-4×8=-32.
故答案为:-32.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目